

Lösung zu B1.1
Im Funktionsterm steht am Wachstumsfaktor ein „hoch x“.
3300 ist der Startwert und der Wachstumsfaktor ist 1,1. Multiplizierst du diesen mit 100, ergibt das 110. Jedes Jahr steigt der Bestand auf 110%, also um 10%. Die richtige Antwort ist 10%.
Hier geht es zur allgemeinen Erklärung:
Lösung zu B1.2
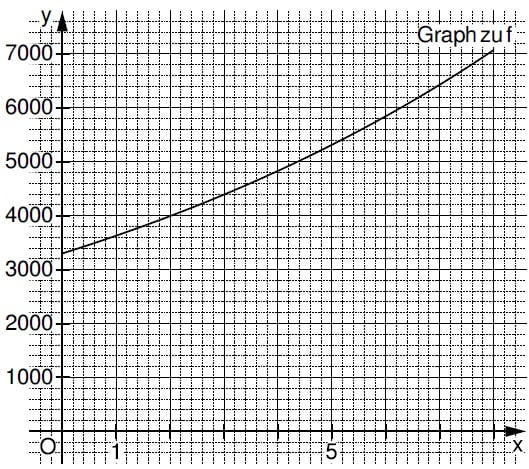
Lass dir im Taschenrechner die Tabelle ausgeben und zeichne dann die Kreuze ins KoSy ein.
Mit dem Taschenrechner berechnest du die Punkte für das Koordinatensystem. Ich habe diese gleich auf Hunderter gerundet.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| x | 3600 | 4000 | 4400 | 4800 | 5300 | 5800 | 6400 | 7100 |
Diese Punkte jetzt so gut es geht ins KoSy zeichnen. An der y-Achse ist ein Kästchen 200!
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.3
Setze für x das passende Zeitintervall in die Funktionsgleichung ein.
\begin{align} x_{ges} &= 2025 – 2011 = 14 \\
f(14) &= 3300 \cdot 1,1^{14} = 12521,7… \approx 12500 \end{align}
Es sind ungefähr 12500 Kegelrobben.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.4
Setze die gesuchte Anzahl für y ein und löse die Gleichung.
\begin{align} y &= 3300 \cdot 1,1^x \,\,\,\,\,\,\,\,\, \text{mit} y = 20000 \\
20000 &=3300 \cdot 1,1^x \,\,\, |:3300 \\
6,06 &= 1,1^x \,\,\, |log_{1,1} ( ) \\
&\Rightarrow x = log_{1,1} (6,06) = 18,90 \text{Jahre} \end{align}
19 Jahre nach 2011 werden über 20.000 Kegelrobben bekannt gegeben, also am 01. Januar 2030.
