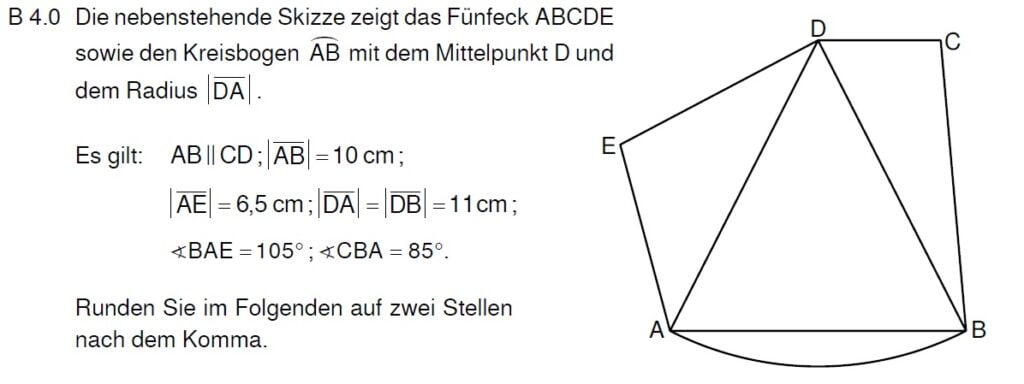

Lösung zu B4.1
Achte beim Geodreieck darauf, dass du die richtige Skala abliest. Am 90°-Winkel kannst du dich orientieren
Die Schritte zur kompletten Zeichnung gibt’s im Video.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.2
Die Vorraussetzung, um die erste Aussage zu begründen, ist die Parallelität von AB und DC. Wenn du mal nicht weiterkommst, überlege dir einen Ansatz mit der letzten Sache, die du ausgerechnet hast.
Aus der Angabe weißt du, dass AB und DC parallel sind. Hier gibt es also besondere Winkel. Die genannten Winkel sind Wechselwinkel und daher maßgleich. So kannst du es aufschreiben:
\( AB||CD \Rightarrow \angle DBA = \angle BDC \) (Wechselwinkel)
Für die Winkel und die Streckenlänge suchst du dir ein Dreieck mit 3 Angaben oder verwendest die Innenwinkelsumme. Wenn du diese besonderen Winkel drauf hast, kannst du auch den Ergänzungswinkel verwenden. Hier in der Lösung gehe ich aber einen anderen Weg.
\begin{align} &\angle DBA \text{ mit dem Cosinussatz im Dreieck ABD:}\\
cos(\angle DBA) &= \frac{|\overline{BD}|^2 + |\overline{AB}|^2 – |\overline{AD}|^2}{2 \cdot |\overline{BD}| \cdot |\overline{AB}|} \\
&= \frac{11^2 + 10^2 – 11^2}{2\cdot 11 \cdot 10} \\
\Rightarrow &\angle DBA = 62,96° \\
\\
&\angle DCB \text{ mit der Innenwinkelsumme im Dreieck:}\\
\angle CBD &= 85° – 62,96° = 22,04° \\
\angle DCB &= 180° – \angle BDC – \angle CBD \\
& = 180° – 62,96° – 22,04° \\
\Rightarrow &\angle DCB = 95° \\
\\
&|\overline{CD}| \text{ mit dem Sinussatz:}\\
\frac{|\overline{CD}|}{sin(\angle CBD)} &= \frac{|\overline{BD}|}{sin(\angle DCB)}\\
\frac{|\overline{CD}|}{sin(22,04°)} &= \frac{11}{sin(95°)} \,\,\, |\cdot sin(22,04°) \\
|\overline{CD}| &= \frac{11}{sin(95°)} \cdot sin(22,04°) \\
\Rightarrow &|\overline{CD}| = 4,14 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.3
Der Umfang ist die Summe aller begrenzenden Strecken und Kreisbögen. Berechne die fehlenden Bestandteile und addiere dann.
\begin{align} \angle DAE &= 105° – 62,96° = 42,04° \\
\\
&|\overline{ED}| \text{ mit dem Cosinussatz im Dreieck ADE}\\
|\overline{ED}|^2 &= |\overline{AE}|^2 + |\overline{AD}|^2 – 2 \cdot |\overline{AE}| \cdot |\overline{AD}| \cdot cos(\angle DAE) \\
&= 6,5^2 + 11^2 – 2 \cdot 6,5 \cdot 11 \cdot cos(42,04°) \\
\Rightarrow &|\overline{ED}| = 7,55 cm \\
\\
&\text{Bogenlänge mit der Formel:}\\
b &= \frac{\angle ADB}{360°}\cdot 2 \cdot r \cdot \pi \\
\\
\angle ADB &= 180° – 2\cdot 62,96° = 54,08° \\
\\
b &= \frac{54,08°}{360°} \cdot 2 \cdot 11 \cdot \pi \\
b &= 10,38 cm \\
\\
&\text{Zusammensetzen zum Umfang}\\
U &= |\overline{AE}| + |\overline{ED}| + |\overline{BD}| + b \\
&= 6,5 + 7,55 + 11 + 10,38\\
\Rightarrow &U = 35,43 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.4
Wenn ein Kreis eine Strecke berührt, dann steht der Radius senkrecht. Du darfst also mit Sin/Cos/Tan rechnen.
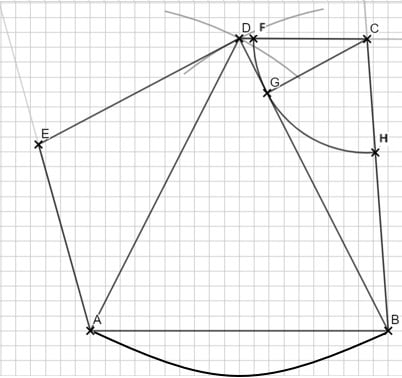
\begin{align} &|\overline{CG}| \text{ mit dem Sinus im Dreieck CDG}\\
sin(\angle BDC) &= \frac{|\overline{CG}|}{|\overline{DC}|}\\
sin(62,96°) &= \frac{|\overline{CG}|}{4,14}\,\,\, |\cdot 4,14 \\
\Rightarrow &|\overline{CG}| = sin(62,96°) \cdot 4,14 = 3,69 cm \\
\\
A_{Sektor} &= \frac{95°}{360°} \cdot 3,69^2 \cdot \pi = 11,29 cm^2 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.5
Der prozentuale Anteil berechnet sich durch Anteil / Ganzes * 100 oder Klein/Groß * 100
\begin{align} A_{BCD} &= \frac{1}{2} \cdot |\overline{BD}| \cdot |\overline{DC}| \cdot sin(\angle BDC) \\
&= \frac{1}{2} \cdot 11 \cdot 4,14 \cdot sin(62,96°)\\
\Rightarrow &A_{BCD} = 20,28 cm^2 \\
\\
p &= \frac{A_{Sektor}}{A_{BCD}} \cdot 100 \% = \frac{11,29}{20,28} \cdot 100 \% = 55,67\% \end{align}
Video wird nochmal aufgenommen
