Lösung zu B3.1
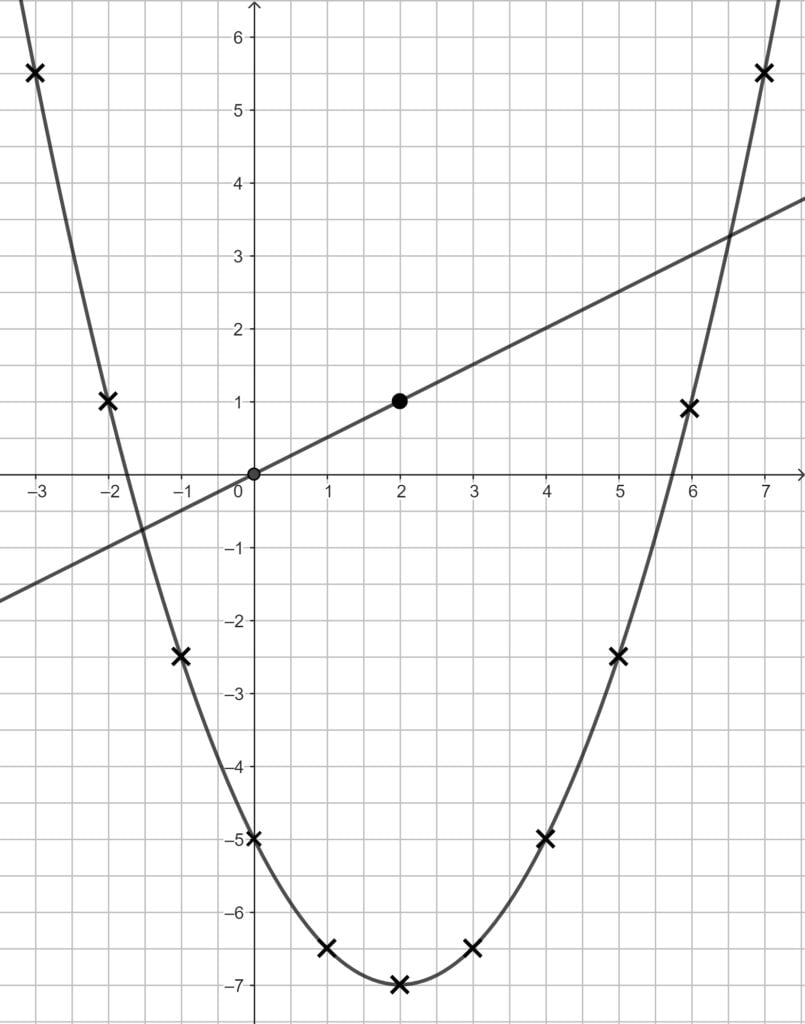
Achtung Spezialfall für die Funktionsgleichung. Scheitelpunkt und Punkt in die Scheitelform einsetzen und a bestimmen. Den Rest musst du selbst hinbekommen!
Eigentlich gilt: Hast du zwei Punkte, arbeitest du mit zwei Gleichung. Außer es ist dieser Spezialfall. Die andere Regel lautet: Hast du den Scheitelpunkt, arbeitest du mit der Scheitelform. Und diese Regel gewinnt.
\begin{align}
y &= a \cdot (x – x_s)^2 + y_s \,\,\,\,\,\,\,\,\, \text{mit } S(2|-7) \\
y &= a \cdot (x – 2)^2 -7\,\,\,\,\,\,\,\,\, \text{mit } P(4|-5) \\
-5 &= a \cdot (4-2)^2 – 7 \\
-5 &= a \cdot 2^2 -7 \\
-5 &= 4a – 7 \,\,\, |+7 \\
2 &= 4a \,\,\, |:4 \\
0,5 &= a \\
\\
&\text{S und a in die Scheitelform einsetzen}\\
y &= 0,5 \cdot (x – 2)^2 – 7 \\
&= 0,5 \cdot (x^2 -4x + 4) – 7 \\
&= 0,5x^2 -2x + 2 – 7 \\
&\Rightarrow y =0,5x^2 -2x – 5 \end{align}
Die Funktionen zeichnest du mit der Tabellenfunktion deines Taschenrechners. Bei der Parabel musst du alle Punkte zeichnen und mit einer Freihandlinie verbinden. Bei der Gerade reichen zwei Punkte und das Lineal. Du kannst dir die Gerade auch mit der Tabelle des TR ausgeben lassen.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.2
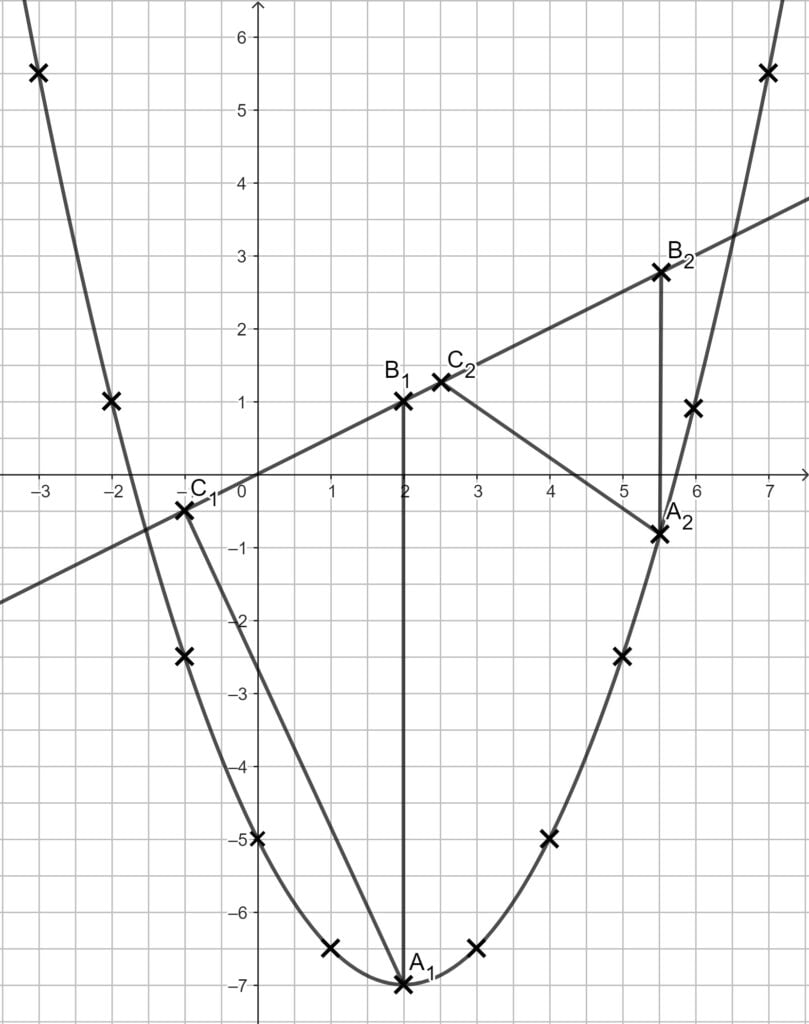
Achtung: 3 LE an der x-Achse weiter links und dann wieder zur Gerade. Nicht mit dem Geodreieck 3 LE an der Geraden entlang.
Du gehst zur passende Stelle für x und zeichnest die Punkte A und B auf den Funktionen ein. Die Punkte C sind dann drei LE weiter links auf der Geraden.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.3
Eine Strecke, die parallel zur y-Achse ist, berechnest du durch „oben-unten“
\begin{align} |\overline{A_nB_n}| &= „oben“ – „unten“ \\
&= 0,5x – (0,5x^2 -2x – 5) \\
&= 0,5x – 0,5x^2 +2x + 5 \\
&\Rightarrow |\overline{A_nB_n}| = (-0,5x^2 + 2,5x + 5) LE \end{align}
Hier geht es zur allgemeinen Erklärung:
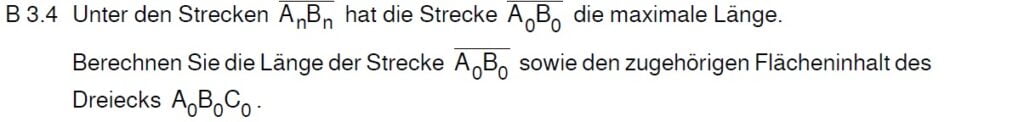
Lösung zu B3.4
Die Aufgabe gibt dir genau die Reihenfolge vor, in der sie leicht zu lösen ist. Taschenrechner und Ergebnis aus 3.3 nicht vergessen!
Mit dem Taschenrechner kannst du das Maximum des Terms aus 3.3 bestimmen. Weil das Dreieck mit diesem Wert den größten Flächeninhalt hat, kannst du damit auch Amax ausrechnen.
\begin{align} &Menü \, \Rightarrow \, A \Rightarrow \, 2 \, \Rightarrow 2 \\
|\overline{A_0B_0}| &= 8,13 LE \,\,\,\,\,\,\,\,\,\,(\text{im Taschenrechner Wert für y)}\\
\\
A_{max} &= \frac{1}{2} \cdot g \cdot h \\
&= \frac{1}{2} \cdot 8,13 \cdot 3 = 12,20 FE\end{align}
Hier geht es zur allgemeinen Erklärung:
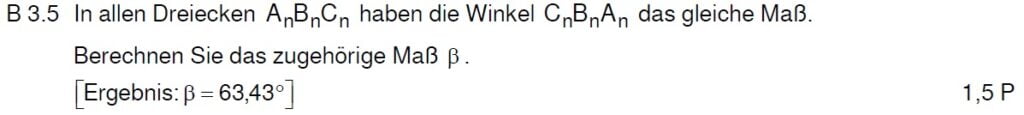
Lösung zu B3.5
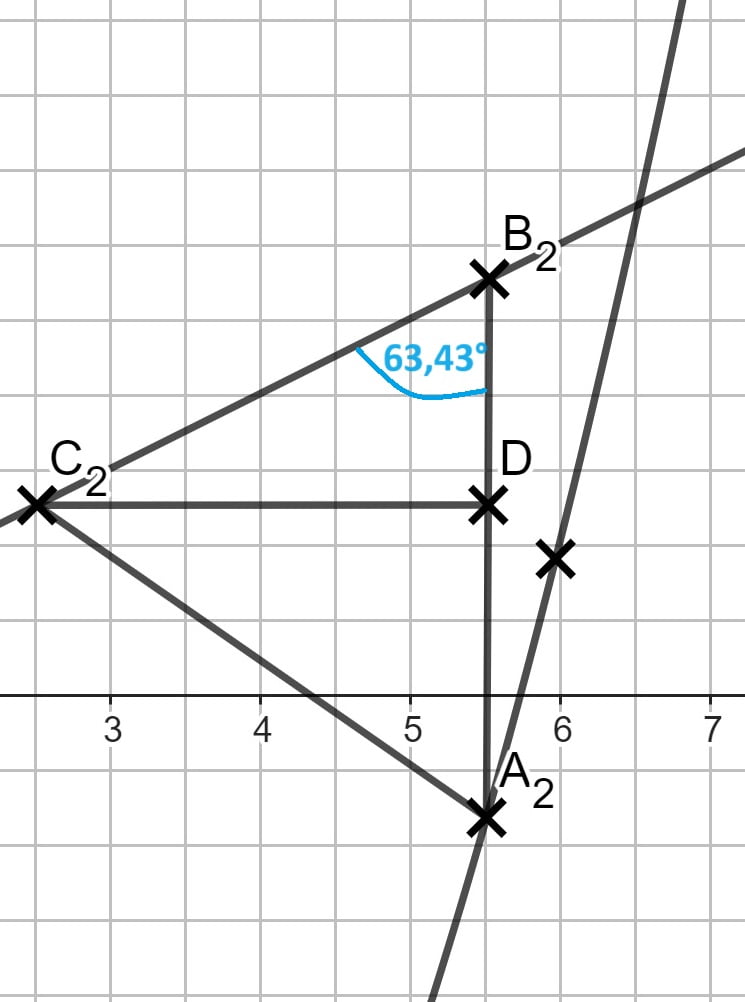
Der Trick hier ist die Gleichung tan(Alpha) = m, wobei m die Steigung der Geraden ist. Das war aber noch nicht alles. Jetzt musst du damit noch auf den richtigen Winkel schließen.
Wenn du die Höhe des Dreiecks einzeichnest, wird es in zwei rechtwinklige Dreiecke zerteilt. Ich habe das hier beim rechten Dreieck als Beispiel gemacht, dass du es dir besser vorstellen kannst. Der Winkel bei C kann mit der Steigung der Geraden berechnet werden. Über die Innenwinkelsumme des Dreiecks kommst du an den gesuchten Winkel bei B.
\begin{align} tan(\angle D_nC_nB_n ) &= m = 0,5 \,\,\, |tan^{-1} \\
\angle D_nC_nB_n &= 26,57° \\
\\
\text{Innenwinkelsumme des Dreiecks CDB}\\
\angle C_n B_n A_n = 180° – 90° – 26,57° = 63,43° \end{align}

Lösung zu B3.6
In 3.5 ist ein Ersatzergebnis gegeben, es muss also etwas mit diesem Winkel zu tun haben.
Erst genau lesen: Die Basis ist \( \overline{AC} \), sie liegt also schräg. Im gleichschenkligen Dreieck sind diese gleich. Das ist immer ein Weg eine Gleichung aufzustellen. Du musst nur für beide Schenkel eine „Formel“ oder deren Länge kennen. Für \(\) |\overline{A_nB_n}|[\latex] kennst du eine Formel aus 3.3. Mit dem Winkel aus 3.5 kannst du \(\) |\overline{B_nC_n}|[\latex] ausrechnen. Im
\begin{align} &|\overline{B_n C_n}| \text{ mit dem Sinus:}\\
sin(\angle C_n B_n A_n) &= \frac{|\overline{C_n D_n}|}{|\overline{B_n C_n}|}\\
sin(63,43°) = \frac{3}{|\overline{B_n C_n}|} \,\,\, &|\cdot |\overline{B_n C_n}| : sin(63,43°) \\
\Rightarrow |\overline{B_n C_n}| &= \frac{3}{sin(63,43°)} = 3,35 cm \\
\\
&\text{Gleichsetzen der Schenkel}\\
|\overline{A_n B_n}| &= |\overline{B_n C_n}| \\
-0,5x^2 +2,5x + 5 &= 3,35 \,\,\,|-3,35 \\
-0,5x^2 + 2,5x + 1,65 &= 0 \end{align}
Taschenrechner Menü A 2 2
\begin{align} x_1 = -0,59 \, &\lor \, x_2 = 5,59 \end{align}