Lösung zu B2.1
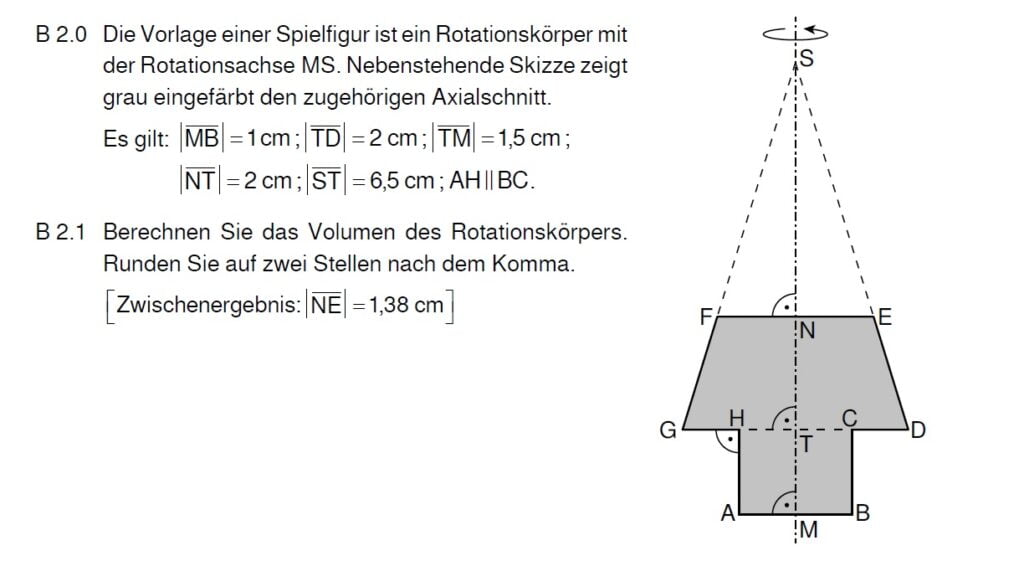
Überlege dir, aus welchen Teilkörpern die Spielfigur besteht. Für die fehlende Streckenlänge brauchst du den Vierstreckensatz.
Die Spielfigur setzt sich aus folgenden Teilkörpern zusammen.
Großer Kegel (GDS)
Kleiner Kegel (FES)
Zylinder (ABCH)
Für den kleinen Kegel benötigst du den Radius des Grundkreises (\( \overline{NE} \)), der mit dem Vierstreckensatz berechnet werden kann.
\begin{align} \frac{|\overline{NE}|} {|\overline{SN}|} &= \frac{|\overline{DT}|}{|\overline{ST}|} \\
\frac{|\overline{NE}|} {4,5} &= \frac{2}{6,5} \,\,\, |\cdot 4,5 \\
|\overline{NE}| &= \frac{2}{6,5}\cdot 4,5 = 1,38cm \\
\\
&\text{Berechnung der Teilkörpervolumina:}\\
V_{großer \, Kegel} &= \frac{1}{3} \cdot |\overline{GT}|^2 \cdot \pi \cdot |\overline{ST}|\\
&= \frac{1}{3} \cdot 2^2 \cdot \pi \cdot 6,5 = 27,23 cm^3 \\
\\
V_{kleiner \, Kegel} &= \frac{1}{3} \cdot |\overline{NE}|^2 \cdot \pi \cdot |\overline{SN}|\\
&= \frac{1}{3} \cdot 1,38^2 \cdot \pi \cdot 4,5 = 8,97 cm^3 \\
\\
V_{Zylinder} &= |\overline{AM}|^2 \cdot \pi \cdot |\overline{AH}| \\
&= 1^2 \cdot \pi \cdot 1,5 = 4,71 cm^3 \\
\\
&\text{ Zusammensetzen zum gesuchten Körper}\\
V_{ges} &= V_{großer \, Kegel} – V_{kleiner \, Kegel} + V_{Zylinder}\\
&= 27,23 – 8,97 + 4,71 \\
&\Rightarrow V_{ges} = 22,97 cm^3 \end{align}
Hier geht es zur allgemeinen Erklärung:
Lösung zu B2.2
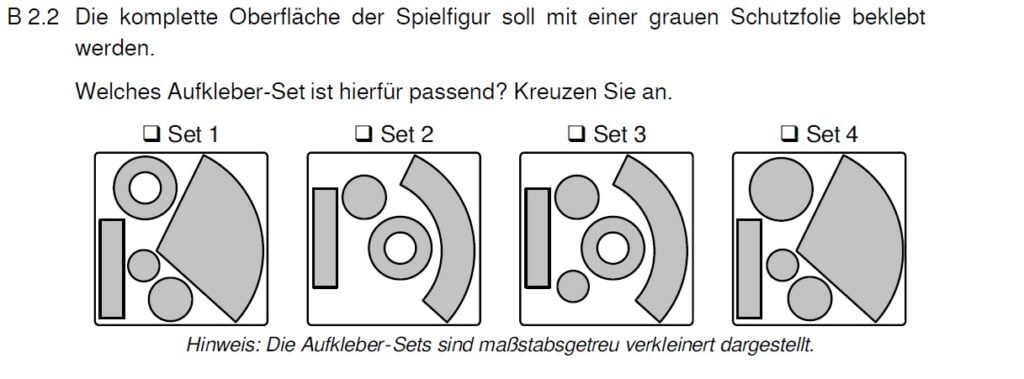
Räumliche Vorstellung ist gefragt! Bestimmt kannst du einige Bilder ausschließen!
Die Figur hat oben und unten einen Kreis. Das zweite und vierte Set kann es also nicht sein, da hier die Kreise nicht passen. Zwischen den Punkten G und H bzw. C und D entsteht ein Kreisring (wie auch im Rotationskörperhack). Dieser ist aber in Set 1 und 3, hilft uns also nicht weiter. Der Kegelstumpf hat als Mantelfläche allerding einen Bogen und keinen Kreissektor. Der Kreissektor ist in Set 1 (falsch). Es bleibt also nur Set 3.
Wenn du es bildlich sehen willst, schaue gerne ins Video!
