

Lösung zu B1.1
Im ersten und zweiten Schritt musst du „S“ und „M“ unterscheiden. Achte darauf, dass sich die Anzahl an Krapfen verändert!
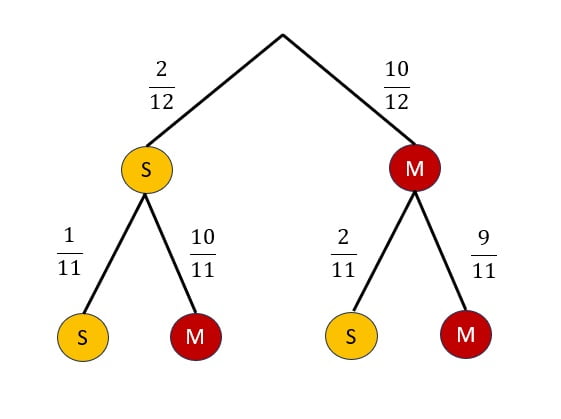
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.2
Überlege dir, welche Kombination an Füllung nicht erlaubt ist. Berechne diese und ziehe von 100% ab.
Achtung: „Mindestens einer der Krapfen mit Senf“ beudetet, dass auch beide mit Senf gefüllt sein dürfen. Die eizige Kombination, die nicht erlaubt ist, ist P(M|M). Berechne diese mit der Pfadregel der Multiplikation und ziehe das Ergebnis von 100% (also ein Bruch gleich Wert 1) ab.
\begin{align} P(M|M) &= P(M_1) \cdot P(M_2) \\
&= \frac{10}{12} \cdot \frac{9}{11} \,\,\,\,\,\,\,\,\,\text{Kürze 9 und 12}\\
&=\frac{10}{4} \cdot \frac{3}{11} \,\,\,\,\,\,\,\,\, \text{Kürze 10 und 4} \\
&=\frac{5}{2} \cdot \frac{3}{11} \\
\Rightarrow &P(M|M) = \frac{15}{22} \\
\\
P_ {ges} &= \frac{22}{22} – \frac{15}{22} = \frac{7}{22} \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.3
Das ist die letzte Teilaufgabe. In 1.2 gibt es ein Ersatzergebnis. Du musst es also hier brauchen!
Aus 1.2 wissen wir, dass mit einer Chance von 7/22 keiner der Krapfen mit Senf ist. „Mindestens einer der Krapfen mit Senf“ bedeutet, dass einer der beiden oder auch beide mit Senf sein dürfen. Es ist also genau das Gegenereignis mit einer Chance von 15/22. Der Taschenrechner verrät dir, dass es 0,681… also ungefähr 68% sind.
Der mathematisch korrekte Anwortsatz ist also: 68% ist weniger als 70%, also hat er nicht recht.
Fragt man mich nicht als Mathe-Lehrer, sondern als Mensch würde ich sagen: Dafür, dass die Aussage völlig unbegründet war, ist das Bauchgefühl von 70% echt gut, da 68% sehr nah dran ist.
