
Lösung zu A1.1
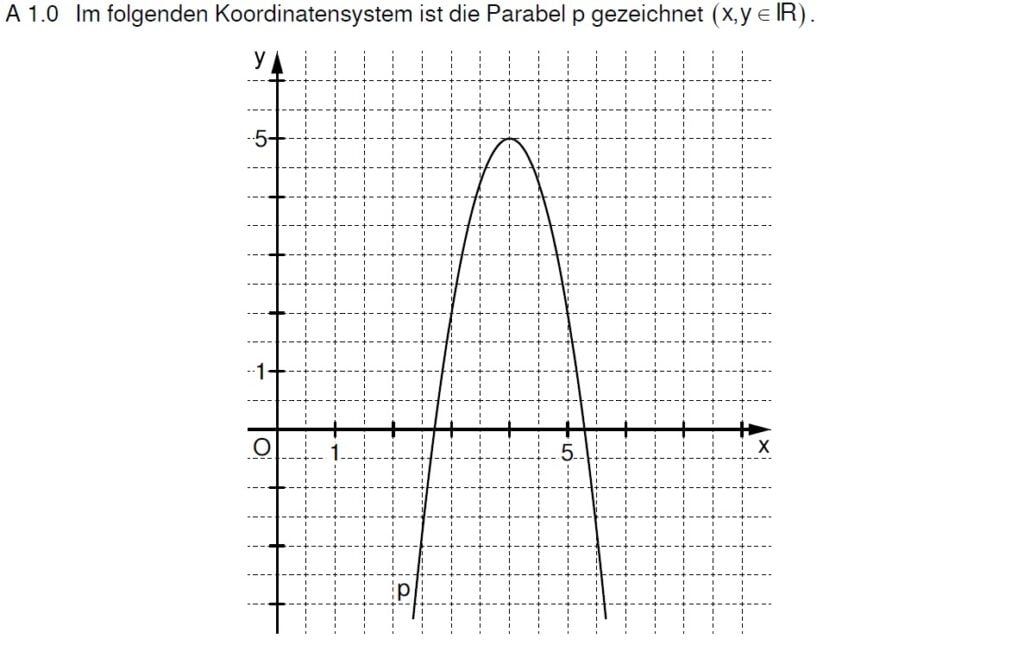
Überlege dir, wie du eine Parabel aus der Scheitelform ohne Taschenrechner zeichnest und gehe diesen Weg andersrum.
Schreibe dir zuerst die Scheitelform auf und versuche dann, die einzelnen Bausteine herauszufinden:
\( y = a \cdot (x – x_S)^2 + y_S \)Der Scheitelpunkt kann aus dem Koordinatensystem abgelesen werden, es ist der höchste Punkt. Also S(4|5) kann schonmal eingesetzt werden,
\( y = a \cdot (x – 4)^2 + 5\)Kommen wir zum schwierigen Teil, der Öffnungsfaktor. Normalerweise würde man „Quadratische Schritte“ gehen. Vom Scheitel 1 ins x Richtung müsste 1² in y-Richtung bedeuten. Da landest du aber nicht auf der Parabel. Wenn du eine LE vom Scheitel nach rechts geht, musst du 3 LE nach unten gehen, um wieder auf der Parabel zu landen. Der Öffnungsfaktor ist also -3. Es folgt:
\( y = -3 \cdot (x – 4)^2 + 5\)Geschafft 🙂
Hier geht es zur allgemeinen Erklärung:

Lösung zu A1.2
Versuche keine verrückte Lösung zu finden. Bei welcher Geraden bist du dir zu 100% sicher? Sie darf auch die Steigung 0 haben.
Natürlich gibt es hier ganz viele Lösungen, aber ich möchte dir erklären, wie du eine einfache Lösung findest.
Dass die Gerade und die Parabel keinen gemeinsamen Punkt haben, muss die Gerade die Parabel passieren. Das ist der Fachbegriff. Oder anders: Sie muss halt daran „vorbeigehen“. Das ist unten ein Problem, da die Parabel dort überall ist. Oben dagegen ist es ab y = 5 kein Problem. Eine Gerade weit oben wird keine Probleme machen. Wenn du eine „witzige“ Anwort suchst:
y = 2x + 100000000000000000000000000000000000000000000000000000000000 löst die Aufgabe.
Jetzt möchtest du vielleicht nicht so viel Zeit mit 0ern verbringen, daher machen wir es uns noch einfacher. Um ganz sicher zu gehen, dass die Gerade keine Probleme macht, soll sie parallel zur x-Achse laufen. Das ist eine Steigung von 0. Jetzt eine „Höhe“ von mehr als 5 und die Aufgabe ist gelöst.
y = 0x + 6
