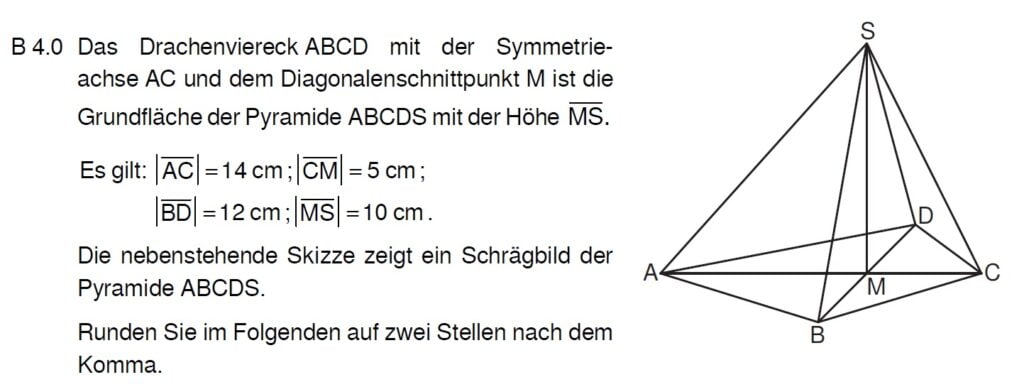

Lösung zu B4.1
Die Höhe steht immer senkrecht, du kannst also Sin/Cos/Tan und SdP verwenden.
\begin{align} &|\overline{CS} \text{ mit dem Satz des Pythagoras:}\\
|\overline{CS}|^2 &= |\overline{CM}|^2 + |\overline{SM}|^2 \\
&= 5^2 + 10^2 \,\,\, |\sqrt{}\\
\Rightarrow &|\overline{CS}| = 11,18 cm \\
\\
&\angle SCA \text{ mit dem Tangens:}\\
tan(\angle SCA) &= \frac{|\overline{SM}|}{|\overline{CM}|}\\
&= \frac{10}{5} \,\,\, |tan^{-1}\\
\Rightarrow& \angle SCA = 63,43° \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.2
Berechne möglichst viele neue Strecken aus der Veränderung.
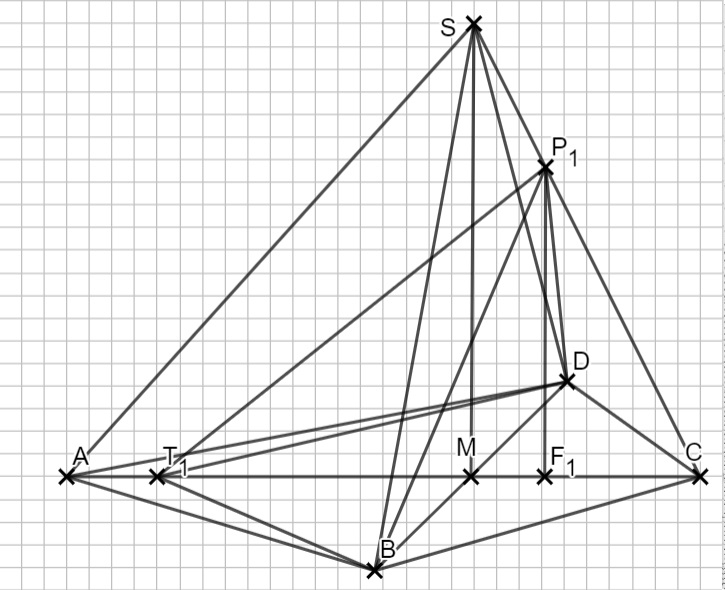
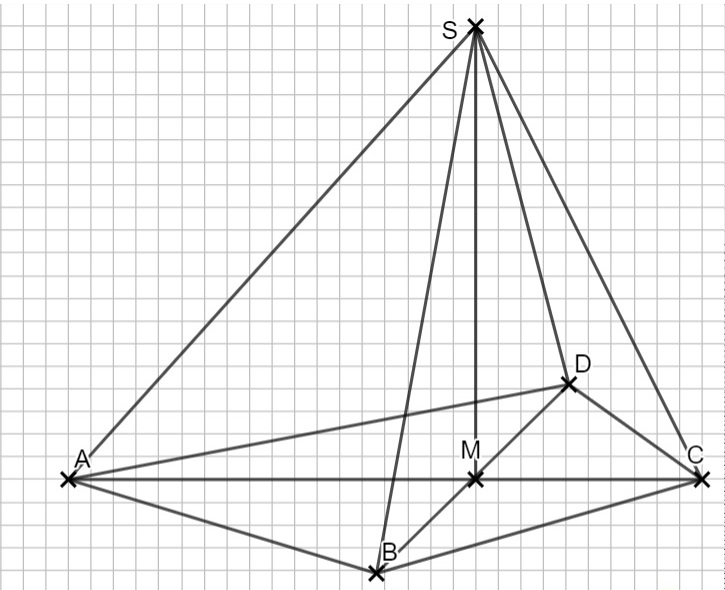
Aus der veränderten Pyramide ergeben sich folgende Längen:
\begin{align}
|\overline{CP_1}| &= 11,18 – 0,5 \cdot 7 = 7,68 cm\\
|\overline{CT_1}| &= 5 + 7 = 12 cm \end{align}
Mit diesen Längen hast du genug Angaben für den Cosinussatz:
\begin{align} |\overline{P_1 T_1}|^2 &= |\overline{CP_1}|^2 + |\overline{CT_1}|^2 – 2 \cdot |\overline{CP_1}| \cdot |\overline{CT_1}| \cdot cos(\angle SCA) \\
&= 7,68^2 + 12^2 -2 \cdot 7,68 \cdot 12 \cdot cos(63,43°) \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{P_1 T_1}| = 10,98 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.3
Wie in 4.1 gilt: Höhen stehen senkrecht. Auch hier kannst du die neue Höhe mit Sin/Cos/Tan oder SdP berechnen.
Für das Volumen der großen Pyramide brauchst du keine weiteren Angaben. Die Höhe der veränderten Pyramide kannst du mit dem Sinus bestimmen.
\begin{align} &V_{ges} \text{ mit der Volumenformel:}\\
V_{ges} &= \frac{1}{3} \cdot A_g \cdot |\overline{MS}|\\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{AC}| \cdot |\overline{BD}| \cdot |\overline{MS}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 14 \cdot 12 \cdot 10 \\
&\Rightarrow 280cm^3 \\
\\
&|\overline{F_1 P_1}| \text{ mit dem Sinus:}\\
sin(\angle SCA) &= \frac{|\overline{F_1 P_1}|}{|\overline{CP_1}|} \\
sin(63,43°) &= \frac{|\overline{F_1 P_1}|}{7,68} \,\,\, |\cdot 7,68 \\
&\Rightarrow |\overline{F_1 P_1}| = 6,87 cm \\
\\
&V_{neu} \text{ mit der Volumenformel:}\\
V_{neu} &= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{CT_1}| \cdot |\overline{BD}| \overline{F_1 P_1}| \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot 12 \cdot 12 \cdot 6,87 \\
&\Rightarrow V_{neu} = 164,88 cm^3 \\
\\
&p \text{ mit der Prozentformel:}\\
p &= \frac{V_{neu}}{V_{ges}} \cdot 100 \% \\
&= \frac{164,88}{280} \cdot 100 \% \\
&\Rightarrow p = 58,89 \% \end{align}
Die neue Pyramide hat 58,89% des großen Volumens, sie ist also um 41,11% kleiner.
Hier geht es zur allgemeinen Erklärung:
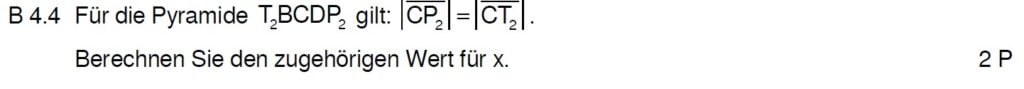
Lösung zu B4.4
Der Ansatz steht schon in der Angabe. Setze für die Streckenlängen pasende Terme ein und löse die Gleichung.
\begin{align} |\overline{CP_2}| &= |\overline{CT_2}| \\
11,18 – 0,5 \cdot x &= 5 + x \,\,\, |-x\\
11,18 – 1,5x &= 5 \,\,\, |-11,18\\
-1,5x &= – 6,18 \,\,\, |:(-1,5) \\
x &= 4,12 \end{align}
Hier geht es zur allgemeinen Erklärung:
Natürlich ist das keine Aufgabe aus der Quadratischen Funktionen, aber das Kapitel „Eigenschaften nachweisen“ hilft hier am meisten weiter.

Lösung zu B4.5
Es gab da einen besonderen Kreis, der etwas mit rechten Winkeln zu tun hatte.
Weil der rechte Winkel bei T liegt, muss T auf dem Thaleskreis mit Mittelpunkt M liegen. Damit gilt:
\( r = |\overline{BM}| = |\overline{BT_3}| = |\overline{MD}| = 6 cm \)
x ist also 6.
Hier geht es zur allgemeinen Erklärung:
Hier hilft nur das Grundwissen. Einfach mal durchlesen und im Kopf behalten.
