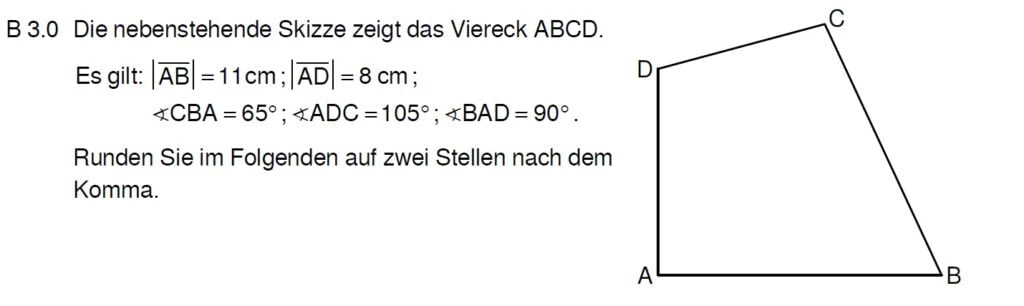

Lösung zu B3.1
Die Innenwinkelsumme gibt es nicht nur im Dreieck, sondern auch im Viereck.
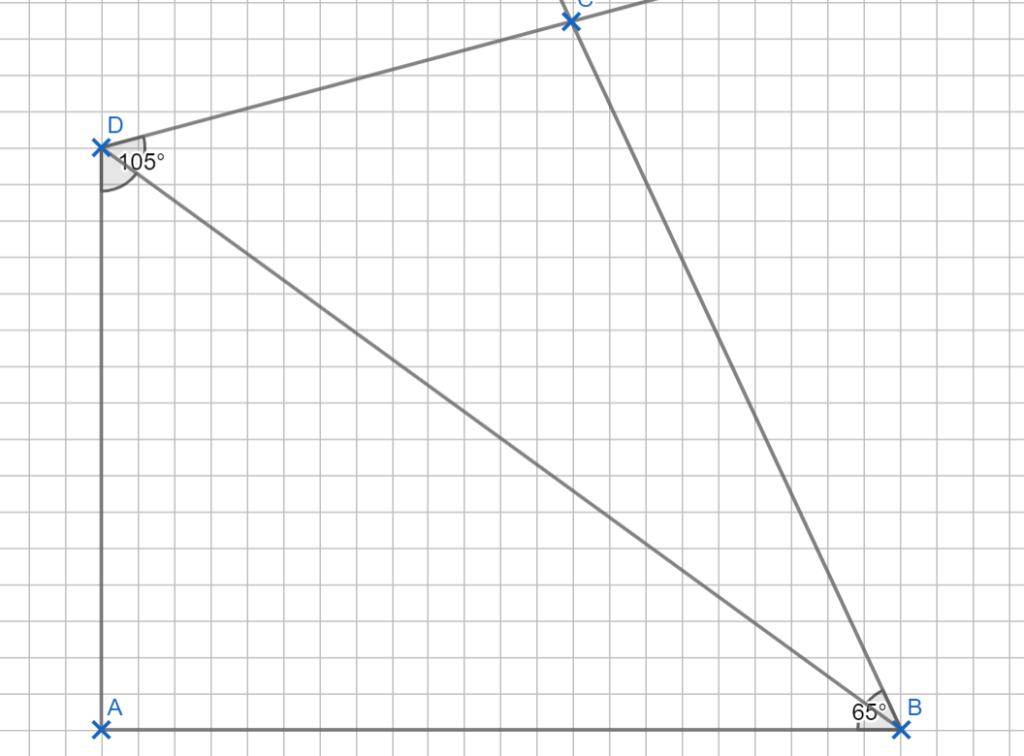
\begin{align} &\angle DCB \text{ über die Innenwinkelsumme:}\\
\angle DCB &= 360° – 65° – 105° – 90° = 100° \\
\\
&|\overline{BD}| \text{mit dem Satz des Pythagoras im Dreieck CBD:}\\
|\overline{BD}|^2 &= |\overline{AB}|^2 + |\overline{AD}|^2 \\
|\overline{BD}|^2 &= 11^2 + 8^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{BD}| = 13,60 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.2
Immer zuerst die Zwischenergebnisse berechnen!
Zuerst immer das Zwischenergebnis berechnen: Du wirst den Winkel CBD brauchen. Du bekommst ihn, indem du vom ganzen Winkel bei B, den unteren abziehst. Diesen kannst du im rechtwinkligen Dreieck bestimmen.
\begin{align} &\angle DBA \text{ im Dreieck ABD:}\\
tan(\angle DBA) &= \frac{|\overline{AD}|}{|\overline{AB}|} \\
&= \frac{8}{11} \,\,\, |tan^{-1}\\
&\Rightarrow \angle DBA = 36,03° \\
\\
\angle CBD &= \angle CBA – \angle DBA \\
&= 65° – 36,03° \\
&\Rightarrow \angle CBD = 28,97° \end{align}
Im Dreieck BCD hast du jetzt alle Angaben, um mit dem Sinussatz \( |\overline{DC}|\) zu berechnen.
\begin{align} &|\overline{DC}| \text{ mit dem Sinususatz im Dreieck BCD:} \\
\frac{|\overline{DC}|}{sin(\angle CBD)} &= \frac{|\overline{BD}|}{sin(\angle DCB)} \\
\frac{|\overline{DC}|}{sin(28,97°)} &= \frac{13,60}{sin(100°)} \,\,\, |\cdot sin(28,97°)\\
|\overline{DC}| &= \frac{13,60}{sin(100°)} \cdot sin(28,97°) \\
&\Rightarrow |\overline{DC}| = 6,69 cm \end{align}
Bleibt noch \( |\overline{BC}|\). Hier bietet sich der Cosinussatz an. Du brauchst du den Winkel BDC, den man leicht über die Innenwinkelsumme im Dreieck bekommt.
\begin{align}
\angle BDC &= 180° – 100° – 28,97° = 51,03° \\
\\
|\overline{BC}|^2 &= |\overline{BD}|^2 + |\overline{DC}|^2 – 2 \cdot |\overline{BD}| \cdot |\overline{DC}| \cdot cos(\angle BDC) \\
&= 13,60^2 + 6,69^2 -2 \cdot 13,60 \cdot 6,69 \cdot cos(51,03°) \,\,\, |\sqrt{} \\
&\Rightarrow |\overline{BC}| = 10,74 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.3
Zerteile in zwei Dreiecke und berechne diese.
Für das allgemeine Viereck gibt es keine Formel. Deshalb zerteilst du in zwei Teildreiecke und berechnest diese einzeln. Im rechtwinkligen Dreieck kannst du \( 0,5 \cdot \text{Kathete} \cdot \text{Kathete} \) verwenden. Im anderen verwendest du die Sinusformel.
\begin{align} A_{ABD} &= 0,5 \cdot |\overline{AB}| \cdot |\overline{AD}| \\
&= 0,5 \cdot 11 \cdot 8 \\
&\Rightarrow A_{ABD} = 44 cm^2 \\
\\
A_{BCD} &= 0,5 \cdot |\overline{BC}| \cdot |\overline{BD}| \cdot sin(CBD) \\
&= 0,5 \cdot 10,74 \cdot 13,60 \cdot sin(28,97°) \\
&\Rightarrow A_{BCD} = 35,37 cm^2 \\
\\
&\Rightarrow A_{ABCD} = A_{ABD} + A_{BCD} = 79,37 cm^2 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.4
Wenn es zu leicht ist, ist es manchmal falsch. Aber nicht immer. Manchmal ist es wirklich leicht.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.5
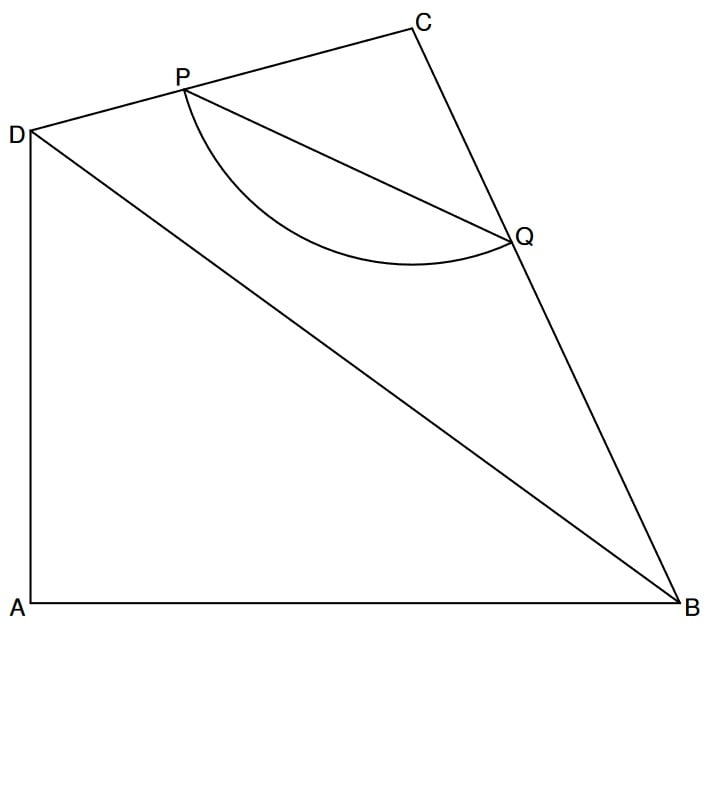
Der Umfang ist die Summe aller Seitenlängen. Hier also die Bogenlänge und eine Strecke.
Der Umfang setzt sich auf dem Kreisbogen und der Streckenlänge \( |\overline{PQ}| \) zusammen. Die Streckenlänge musst du zuerst mit dem Cosinussatz berechnen.
\begin{align} &|\overline{PQ}| \text{ mit dem Cosinssatz:}\\
|\overline{PQ}|^2 &= r^2 + r^2 – 2 \cdot r \cdot r \cdot cos(\angle DCB) \\
&= 4^2 + 4^2 – 2 \cdot 4 \cdot 4 \cdot cos(100°) \,\,\, |\sqrt{} \\
&\Rightarrow |\overline{PQ}| = 6,13 cm \\
\\
&b \text{ mit der Bogenlängen-Formel:}\\
b &= \frac{\angle DCB}{360°} \cdot 2 \cdot r \cdot \pi \\
&= \frac{ 100°}{360°} \cdot 2 \cdot 4 \cdot \pi \\
&\Rightarrow b = 6,98 cm \\
\\
&\Rightarrow u = b + |\overline{PQ}| = 6,98 + 6,13 = 13,11 cm \end{align}

Lösung zu B3.6
Achtung, es geht nicht um den Kreissektor, sondern um das Segment! Den Flächeninhalt vom Dreieck musst du also abziehen.
Zuerst berechnest du den Flächeninhalt des Kreissegments, um dann den prozentualen Anteil zu bestimmen.
\begin{align} &\text{Segment durch Sektor – Dreieck:}\\
A &= A_{\text{Sektor}} – A_{CPQ}\\
&= \frac{\angle DCB}{360°} \cdot r^2 \cdot \pi – 0,5 \cdot r \cdot r \cdot sin(\angle DCB)\\
&= \frac{100°}{360°} \cdot 4^2 \cdot \pi – 0,5 \cdot 4 \cdot 4 \cdot sin(100°) \\
&\Rightarrow A = 6,08 cm^2 \\
\\
&p \text{ mit der Prozentformel:}\\
p &= \frac{Anteil}{Ganzes} \cdot 100\% = \frac{ 6,08}{79,37} \cdot 100\% = 7,66\% \end{align}
