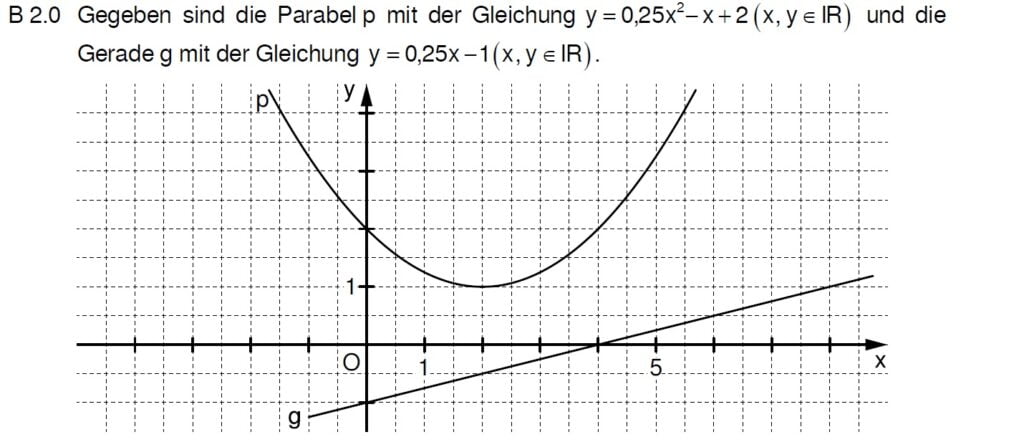

Lösung zu B2.1
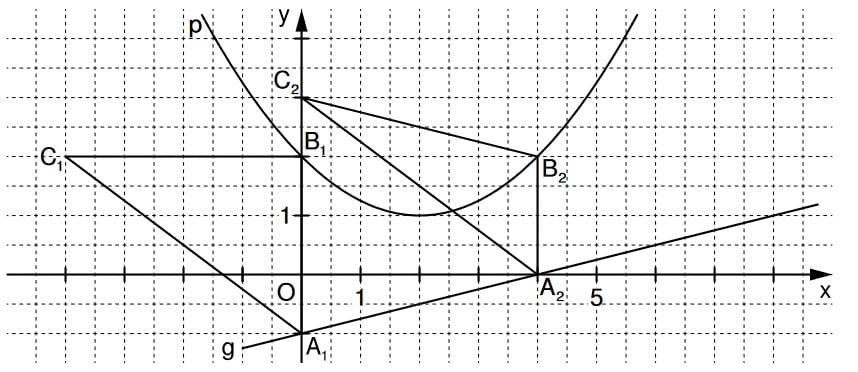
Der Vektor zeigt vom Punkt A zum Punkt C. Von A -4 LE in x-Richtung und 3 LE in y-Richtung. Dort findest du C.
Hier geht es zur allgemeinen Erklärung:
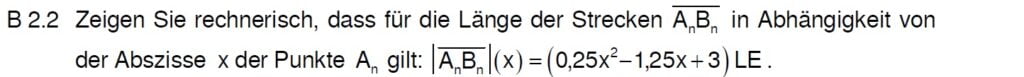
Lösung zu B2.2
A und B haben diesselbe Abszisse. Rechne „oben – unten“
\begin{align}
|\overline{A_n B_n}|(x) &= „oben – unten“ \\
&= 0,25x² – x + 2 – (0,25x -1) \\
&= 0,25x² – x + 2 – 0,25x + 1 \\
\Rightarrow &|\overline{A_n B_n}|(x) =( 0,25x² – 1,25x + 3 ) LE \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.3
Bei gleichschenkligen Dreiecken sind zwei Seiten gleichlang. Damit kannst du eine Gleichung aufstellen. Die zweite Seite bekommst du aus dem Vektor.
Genau lesen: Gleichschenklig mit Basis \( \overline{BC} \). Die anderen beiden Seiten sind also gleichlang.
Oder als Formel ausgedrück:
\(|\overline{AB}| = |\overline{AC}| \)
Auf der linken Seite setzt du die Formel aus 2.2 ein, auf der rechten Seite berechnest du die Länge mit dem Satz des Pythagoras us den koordinaten des Vektors:
\begin{align}|\overline{AB}| &= |\overline{AC}| \\
0,25x² – 1,25x + 3 &= 5 \,\,\, |-5 \\
0,25x² – 1,25x – 2 &= 0 \\
&\Rightarrow \text{TR; Menü A; 2; 2}\\
&\Rightarrow x_1 = -1,27 \lor x_2 = 6,27 \end{align}
