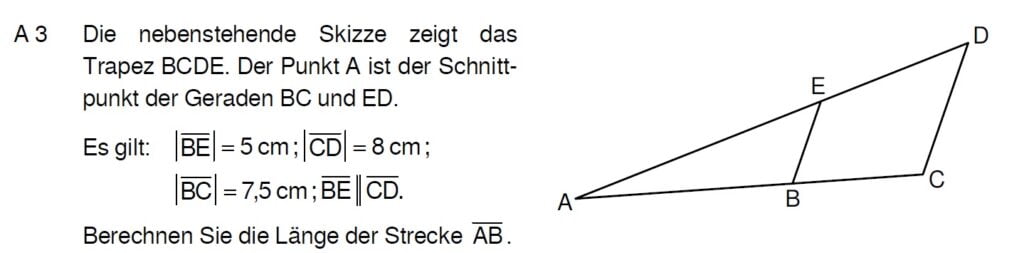
Lösung zu A3
Es gibt Parallelen, das ist immer ein Hinweis auf den Vierstreckensatz.
Der Ansatz ist bestimmt klar: Vierstreckensatz. Leider ist die Gleichung ohne Taschenrechner schwer zu lösen.
Löse den Bruch auf, indem du die Gleichung mit dem Nenner multiplizierst (Zeile 3), dann geht es.
\begin{align}
\frac{|\overline{AB}|}{|\overline{AC}|} &= \frac{\overline{BE}|}{|\overline{CD}|} \\
\frac{|\overline{AB}|}{|\overline{AB}| + 7,5} &= \frac{5}{8} \,\,\, |\cdot (|\overline{AB}| + 7,5)\\
|\overline{AB}| &= \frac{5}{8} \cdot (|\overline{AB}| + 7,5) \,\,\, |\cdot 8 \\
8 \cdot |\overline{AB}| &= 5 \cdot (|\overline{AB}| + 7,5) \\
8 |\overline{AB}| &= 5|\overline{AB}| + 37,5 \,\,\, |-5|\overline{AB}| \\
3 |\overline{AB}| &= 37,5 \,\,\, |:3 \\
\Rightarrow & |\overline{AB}| = 12,5 cm \end{align}
Hier geht es zur allgemeinen Erklärung:
Die beste Erklärung gibt es im Grundwissen: https://map-hack.de/grundwissen/vierstreckensatz/
Wenn du mehr Aufgaben zum Rechnen in der ebenen Geometrie suchst, dann geht es hier entlang:
