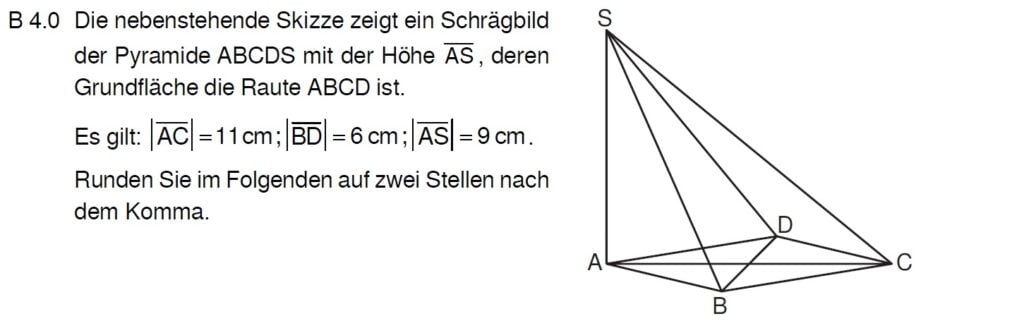

Lösung zu B4.1
Die Höhe steht immer senkrecht auf die Grundfläche. Du kannst also mit Sin/Cos/Tan und dem SdP rechnen.
\begin{align} &|\overline{CS}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{CS}| ^2 &= |\overline{AS}|^2 + |\overline{AC}|^2 \\
&= 9^2 + 11^2 \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{CS}| = 14,21 cm \\
\\
&\angle SCA \text{ im Dreieck ACS mit dem Tangens:}\\
tan(\angle SCA) &= \frac{|\overline{AS}|}{|\overline{AC}|}\\
&= \frac{9}{11} \,\,\, |tan^{-1} \\
&\Rightarrow \angle SCA = 39,29° \end{align}
Hier geht es zur allgemeinen Erklärung:

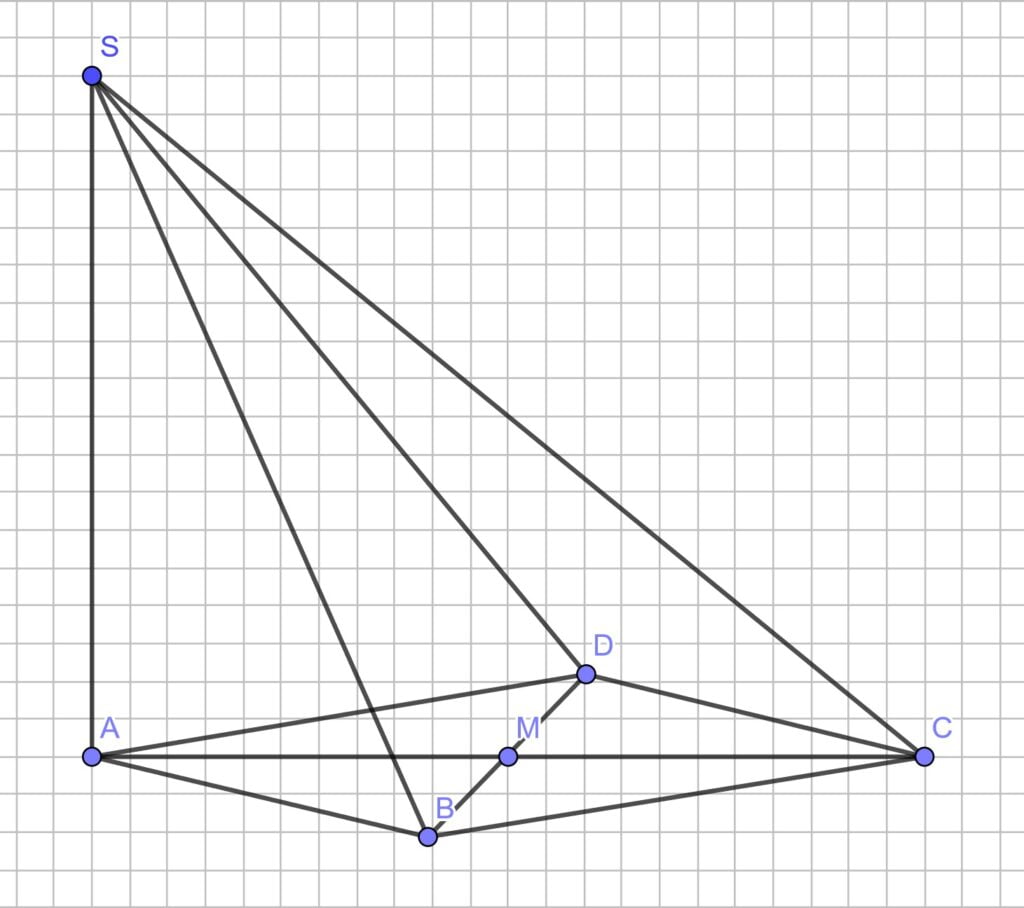
Lösung zu B4.2
Du kannst den gesuchten Winkel nicht direkt berechnen. Fang doch einfach mit dem Ersatzergebnis an.
Falls du mit dem Sinussatz arbeitest, achte auf den Spezialfall.
Für diese Aufgabe gibt es viele Rechenwege. Wenn du einen Weg über den Sinussatz gehst, musst du den Sonderfall beachten.
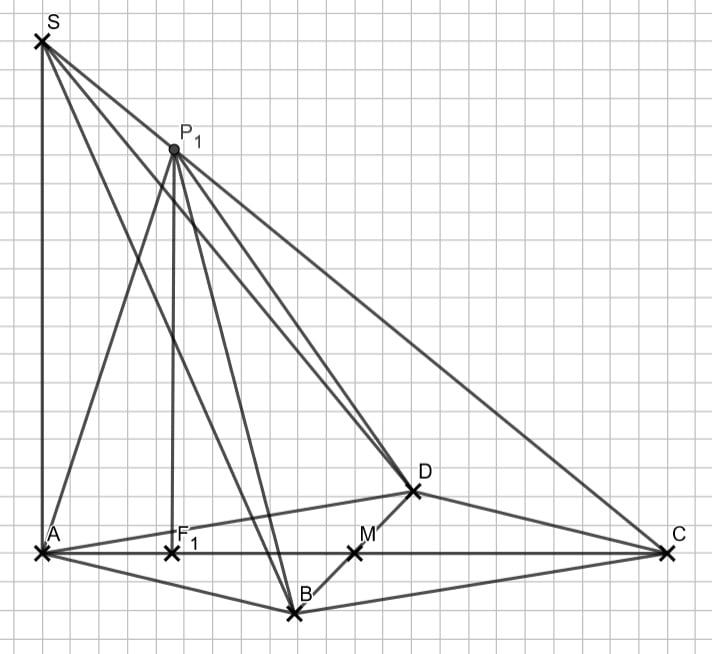
Weil ich diesen gerne vergesse, gehe ich über den Cosinussatz. Dazu brauchst du zuerst die Länge die Strecke \( \overline{AP_1} \), die man im Dreieck ACP1 ausrechnen kann.
\begin{align} &|\overline{AP_1}| \text{ mit dem Cosinussatz im Dreieck ACP:}\\
\\
\text{Es gilt:} & |\overline{CP_1}| = 14,21 – 3 = 11,21 cm \\
|\overline{AP_1}|^2 &= |\overline{AC}|^2 + |\overline{CP_1}|^2 – 2 \cdot |\overline{AC}| \cdot |\overline{CP_1}| \cdot cos(39,29°) \\
&= 11^2 + 11,21^2 – 2 \cdot 11 \cdot 11,21 \cdot cos(39,29°) \,\,\, |\sqrt{}\\
&\Rightarrow |\overline{AP_1}| = 7,47 cm \\
\\
&\angle SP_1A \text{ mit dem Cosinussatz:}\\
cos(\angle SP_1A) &= \frac{|\overline{SP_1}|^2 + |\overline{AP_1}|^2 – |\overline{AS}|^2}{2 \cdot |\overline{SP_1}| \cdot |\overline{AP_1}|}\\
&= \frac{3^2 + 7,47^2 – 9^2}{2 \cdot 3 \cdot 7,47}\,\,\, |cos^{-1} \\
&\Rightarrow \angle SP_1A = 111,19° \end{align}
Hier geht es zur allgemeinen Erklärung:
Komplizierte Berechnungen sind im Ebene-Geometrie-Hack erklärt. Der rechte Button führt also nicht in die Raumgeomtrie, ist aber richtig.

Lösung zu B4.3
Achtung, welche Grundfläche hat die neue Pyramide? Die Höhe in Abhängigkeit von x kannst du z.B. mit dem Vierstreckensatz bestimmen.
Achtung, Beschriftung beachten. Die neue Pyramide hat nur das „halbe Dreieck“ ABD als Grundfläche.
Hier hast du alle Angaben, aber die Höhe h(x) musst du noch berechnen. Das machst du im Dreieck \( CP_nF_n \) mit dem Sinus oder mit dem Vierstreckensatz machen.
\begin{align} &|\overline{P_n F_n}| \text{ mit dem Sinus:}\\
sin(\angle SCA) = \frac{|\overline{P_n F_n}|}{|\overline{CP_n}|} \\
sin(39,29°) &= \frac{ |\overline{P_n F_n}|}{14,21 – x } \,\,\, |\cdot (14,21 – x) \\
sin(39,29°) \cdot (14,21 – x) &= |\overline{P_n F_n}| \\
0,63 \cdot (14,21 – x) &= |\overline{P_n F_n}| \\
|\overline{P_n F_n}| &= 8,95 – 0,63x \\
\\
&\text{Einsetzen in die Volumenformel:}\\
V(x) &= \frac{1}{3} \cdot A_g \cdot h \\
&= \frac{1}{3} \cdot (0,5 \cdot |\overline{AM}| \cdot |\overline{BD}|) \cdot |\overline{P_n F_n}|\\
&= \frac{1}{3}\cdot (0,5 \cdot 5,5 \cdot 6) \cdot (8,95 – 0,63x)\\
&= 5,5 \cdot (8,95 – 0,63x) \\
&\Rightarrow V(x) = 49,23 – 3,47x = (- 3,47x + 49,23) cm^3 \end{align}
Das Ergebnis stimmt nicht mit dem Ergesatzergenis überein, da die Müsterlösung mit dem Vierstreckensatz gerechnet wurde und dort andere Rundungsfehler entstehen. Wenn man sin(39,29°) nicht auf zwei Stellen rundet, sondern z.B. auf 3, wird das Ergebnis besser.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.4
Um 80% kleiner, es bleiben also 20%. Setze diesen Wert mit dem Term aus 4.3 gleich.
Zuerst berechnest du das Volumen der großen Pyramide. Die kleine Pyramide soll UM 80% kleiner sein, also 20% des großen Volumens sein.
Setze 20% des großen Volumens mit dem Term aus B4.3 gleich und löse mit dem Taschenrechner.
\begin{align}
V_{ABCDS} &= \frac{1}{3} \frac{1}{2} \cdot |\overline{AC}| \cdot |\overline{BD}| \cdot |\overline{AS}| \\
&= \frac{1}{3} \frac{1}{2} \cdot 11 \cdot 6 \cdot 9 \\
&\Rightarrow V_{ABCDS} = 99 cm^3 \\
\\
V(x) &= 0,2 \cdot V_{ABCDS} \\
-3,47x + 49,5 &= 0,2 \cdot 99 \,\,\, |-49,5 \\
-3,47x &= -29,7 \,\,\, |:(-3,47) \\
x & = 8,56 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B4.5
Wann ist das Volumen am größsten? Schreibe dir die Formel für das Pyramidenvolumen allgemein auf und schreibe für jeden Faktor, wie er im Vergleich zur großen Pyramide ist.
Das Volumen ist nur von der Höhe abhängig, weil die Grundfläche gleich bleib. Die größte Höhe entsteht also, wenn P auf S liegt. Dann sind die Höhen der beiden Pyramiden gleich.
Weil die Grundfläche der kleinen Pyramide die Hälfte der größen Pyramide ist, gilt das auch für die Volumina. Fertig 🙂
Mit etwas mehr Rechnung kann die Aufgabe auch gelöst werden. Das größte Volumen entsteht für x = 0. Setze in den Term aus 4.3 ein und bestimme den Anteil:
\begin{align} V(0) &= -4,37 \cdot 0 + 49,5 = 49,5 \\
\frac{V(0)}{V_{ABCDS}} &= 49,5/99 = 0,5 = 50 \% \end{align}
