

Lösung zu B3.1
Du hast zwei Punkte gegeben, also musst du mit zwei Gleichungen ansetzen – einem Gleichungssystem.
Du hast zwei Punkte gegeben, also arbeitest du mit zwei Gleichungen. Du setzt die x-Koordinate in die x der Funktionsgleichung ein, mit y genauso.
Anschließend formst du um, dass der TR das Gleichungssystem lösen kann.
\begin{align}
(I) y &= -0,25x^2 + bx + c \,\,\, \text{ mit } P(6|6)\\
&(II) y = -0,25x^2 + bx + c \,\,\, \text{ mit } Q(8|3) \\
\\
(I) 6 &= -0,25 \cdot 6^2 + b \cdot 6 + c \\
&(II) 3 = -0,25 \cdot 8^2 + b \cdot 8 + c \\
\\
(I) 6 &= -9 + 6b + c \,\,\, |+9 \\
&(II) 3 = -16 + 8b + c \,\,\, |+16 \\
\\
(I) 15 &= 6b + c \\
&(II) 19 = 8b + c \\
\\
\text{ TR -> Mode A -> 1 -> 2}\\
\\
b = 2 ; c = 3 \end{align}
Die Funktionen zeichnest du mit der Tabellenfunktion deines Taschenrechners. Bei der Parabel musst du alle Punkte zeichnen und mit einer Freihandlinie verbinden. Bei der Gerade reichen zwei Punkte und das Lineal.
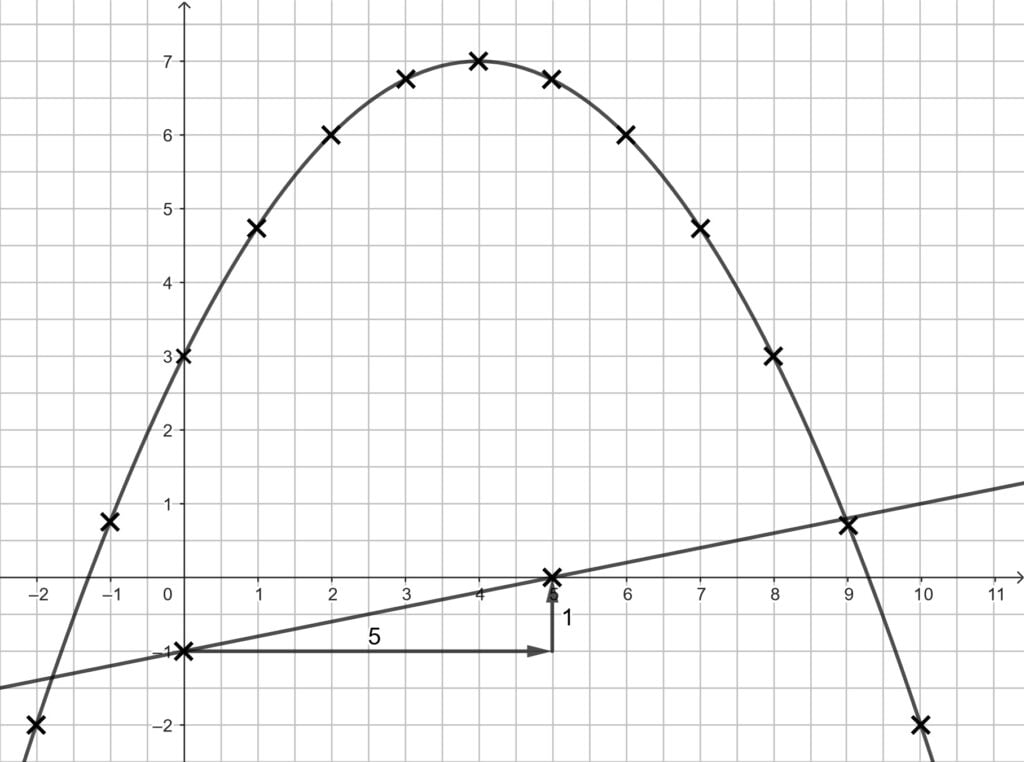
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.2
Gleichseitige Dreiecke haben 3 gleiche Winkel. Die 180° Innenwinkelsumme verteilt sich also gleichmäßig. Mit den beiden Winkeln bei A und C kannst du B finden.
Du gehst zur passende Stelle für x und zeichnest die Punkte A und C auf den Funktionen ein. Weil die Dreiecke gleichseitig sein sollen, kannst du jeweils einen 60° Winkel einzeichnen und im Schnittpunkt B finden. Alternativ kannst du deinen Zirkel verwenden.
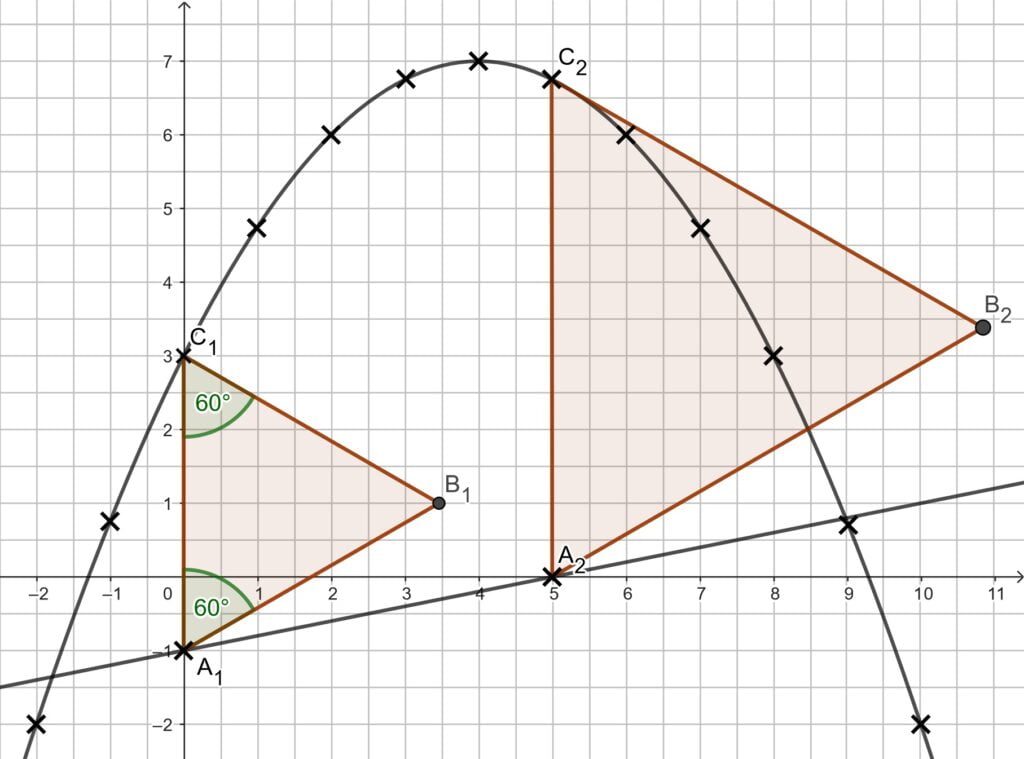
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.3
Das Intervall wird durch bie Schnittpunkte der Funktionen begrenzt.
Um die Intervallgrenzen zu bestimmen, setzt du die Funktionsterme gleich und löst nach „=0“ auf. Anschließend löst du die Gleichung mit dem Taschenrechner.
\begin{align} y_{Gerade} &= y_{Parabel} \\
\frac{1}{5}x – 1 &= -0,25x^2 +2x + 3 \,\,\, | -\frac{1}{5}x + 1 \\
0 &= -0,25x^2 + 1,8x + 4 \\
\text{ TR -> Mode A -> 2 -> 2 }\\
x_1 = -1,78 &\lor x_2 = 8,98 \\
\Rightarrow &x \in ]-1,78 ; 8,98[ \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.4
A und C haben diesselbe Abszisse, du darfst also „oben – unten“ rechnen.
Weil die Punkte A und C dieselbe Abszisse haben, kannst du die Länge der Strecke durch „oben – unten“ berechnen“.
\begin{align} &|\overline{A_n C_n}| (x) \text{ durch „oben – unten“}\\
|\overline{A_n C_n}| (x) &= y_{Parabel}- y_{Gerade} \\
&= -0,25x^2 +2x + 3 – (\frac{1}{5} x – 1 ) \\
&= -0,25x^2 + 2x + 3 – \frac{1}{5}x + 1 \\
\Rightarrow & |\overline{A_n C_n}| (x) = (-0,25x^2 + 1,8x + 4) LE \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.5
An die maximale Streckenlänge kommst du durch den Term aus der Aufgabe B3.4 und dem Taschenrechner. Für gleichseitige Dreiecke findest du dann eine Formel in deiner Formelsammlung.
Die maximale Länge bestimmst du mit dem Taschenrechner und dem Term aus 3.4.
Dieses Ergebnis kannst du in die Formel für den Flächeninhalt des gleichseitigen Dreiecks einsetzen.
Mode A -> 2 -> 2
\begin{align} |\overline{A_0 C_0}|&= 7,24 LE \text{ für } x = 3,6 \\
\
&\text{ Einsetzen in die Flächenformel:}\\
A &= \frac{|\overline{A_0 C_0}|^2}{4} \cdot \sqrt{3} \\
&= \frac{7,24^2}{4} \cdot \sqrt{3} \\
\Rightarrow &A = 22,70 FE \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B3.6
Bei Geraden und Winkeln gibt es einen Zusammenhang mit dem Tangens. Suche mal in deiner Formelsammlung.
Die Gerade g schließt mit der x-Achse einen Winkel ein, den du über die Steigung bestimmen kannst.
Der Winkel BAC ist immer 60°, da das Dreieck gleichseitig ist. Die x-Achse und die y-Achse stehen senkrecht aufeinander. Daraus kannst du dir den gesuchen Winkel zusammenbasteln.
\begin{align}
&\alpha \text{ zwischen Gerade und x-Achse:}\\
tan(\alpha) &= m \\
&= \frac{1}{5} \,\,\, |tan^{-1}\\
\Rightarrow & \alpha = 11,31° \\
\\
\Phi &= 90° – 60° – 11,31° = 18,69° \end{align}
