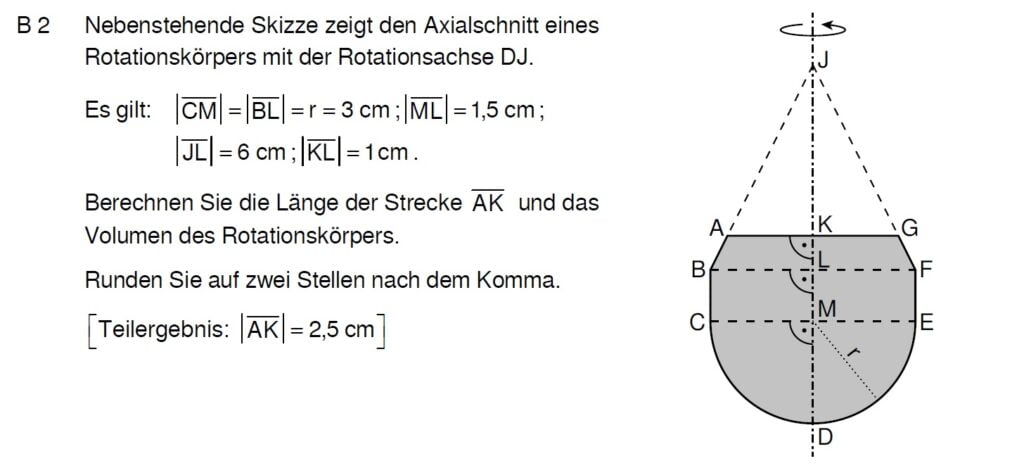
Lösung zu B2
Bei parallelen Strecken kann man es immer mal mit dem Vierstreckensatz probieren.
Die Strecke \( \overline{AK}\) kannst du mit dem Vierstreckensatz bestimmen, denn wegen den rechten Winkel gilt: AG||BF
\begin{align} \frac{|\overline{AK}|}{|\overline{BL}|} &= \frac{|\overline{JK}|}{|\overline{JL}|} \\
\frac{|\overline{AK}|}{3} &= \frac{5}{6} \,\,\, |\cdot 3 \\
\Rightarrow &|\overline{AK}| = 2,5 cm \end{align}
Der Rotationskörper setzt sich von unten nach oben aus einer Halbkugel, einem Zylinder und einem Kegelstumpf (großer Kegel minus kleiner Kegel) zusammen.
Du hast alle Angaben, kannst also einsetzen und losrechnen.
\begin{align}
V_{Halbkugel} &= 0,5 \cdot \frac{4}{3} \cdot |\overline{CM}|^3 \cdot \pi \\
&= 0,5 \cdot \frac{4}{3} \cdot 3^3 \cdot \pi \\
&\Rightarrow V_{Halbkugel} = 56,55 cm^3 \\
\\
V_{Zylinder} &= \pi \cdot |\overline{CM}|^2 \cdot |\overline{LM}| \\
&= \pi \cdot 3^2 \cdot 1,5 \\
&\Rightarrow V_{Zylinder} = 42,41 cm^3 \\
\\
V_{großer Kegel} &= \frac{1}{3} \cdot \pi \cdot |\overline{BL}|^2 \cdot |\overline{JL}|\\
&= \frac{1}{3} \cdot 3^2 \cdot \pi \cdot 6 \\
&\Rightarrow V_{großer Kegel} = 56,55 cm^3 \\
\\
V_{kleiner Kegel} &= \frac{1}{3} \cdot \pi \cdot |\overline{AK}|^2 \cdot |\overline{JK}|\\
&= \frac{1}{3} \cdot \pi \cdot 2,5^2 \cdot 5 \\
&\Rightarrow V_{kleiner Kegel} = 32,72 cm^3 \\
\\
V_{ges} &= 56,55 + 42,41 + 56,55 – 32,72 = 122,79 cm^3 \end{align}
