

Lösung zu B1.1
Achte beim Geodreieck darauf, ob du gerade 40°, 50° oder 100° einzeichnest. Mache den Doppelcheck, indem du für einen anderen Winkel sein Maß überlegst und dann misst.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.2
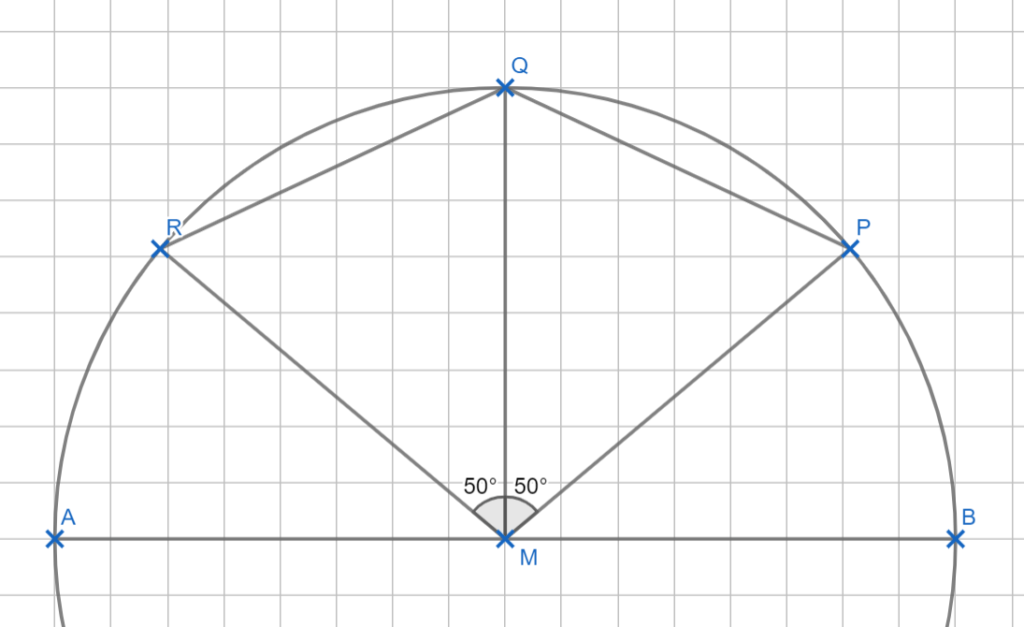
Alle Verbindungslinien des Mittelpunkts M mit der Kreislinien sind Radien und damit kennst du deren Streckenlängen.
Alle Strecken vom Mittelpunkt M aus zur Kreislinie sind Radien und damit 4 cm lang. Die Strecke \(\overline{RM} \) ist 4 cm lang, genauso wie \(\overline{QM} \) .
kannst du im Dreieck MQR mit dem Cosinussatz rechnen.
\begin{align} &|\overline{RQ}| \text{ mit dem Cosinussatz:}\\
|\overline{RQ}|^2 &= |\overline{RM}|^2 + |\overline{QM}| – 2 \cdot |\overline{RM}| \cdot |\overline{QM}| \cdot cos(\angle QMR) \\
&= 4^2 + 4^2 – 2 \cdot 4 \cdot 4 \cdot cos(50°)\,\,\, |\sqrt{}\\
\Rightarrow &|\overline{RQ}| = 3,38 cm \\
\\
&\text{Einsetzen in die Umfangsformel:}\\
u &= 2 \cdot |\overline{RM}| + 2 \cdot |\overline{RQ}|\\
&= 2 \cdot 4 + 2\cdot 3,38 \\
\Rightarrow & u = 14,76 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B1.3
Die große Figur besteht aus einem Halbkreis und dem Durchmesser. Addiere die beiden Streckenlängen und verwende dann Prozentrechnung.
Zuerst berechnest du die Umfang der großen Figur. Er setzt sich aus dem Halbkreisbogen und dem Durchmesser zusammen.
Anschließend berechnest du den Anteil (Drachenviereck) vom Ganzen (Halbkreis).
\begin{align} &\text{ Umfang des Halbkreises:}\\
u_{Hk} &= |\overline{AB}| + 0,5 \cdot 2 \cdot |\overline{AM}| \cdot \pi \\
&= 8 + 0,5 \cdot 2 \cdot 4 \cdot \pi \\
\Rightarrow &u_{Hk} = 20,57 cm\\
\\
&\text{Berechnung des prozentualen Anteils:}\\
p &= \frac{u_{Drache}}{u_{Hk}} = \frac{14,76}{20,57} = 0,7175 = 71,75 \% \end{align}
