Lösung zu A3.1
Für jede Taste hast du die Möglichkeiten C, D, E, G und A. Viermal wird die Auswahl daraus getroffen.
Es gibt 5 verschiedene Tasten, die zufällig gewählt werden. Die Tasten können mehrfach gewählt werden, also bleibt die Anzahl an Möglichkeiten erhalten.
In jedem der vier Schritte gibt es also 5 Möglichkeiten.
\(5 \cdot 5 \cdot 5 \cdot 5 = 5 \cdot 125 = 625 \)
Hier geht es zur allgemeinen Erklärung:

Lösung zu A3.2
Es ist die Frage nach einer einzigartigen Kombination aus 625 möglichen.
Für jede vorgegebenen Tastenanschlag gibt es eine Chance von \(\frac{1}{5} \).
\begin{align} P(A – C – D – C) &= P(A) \cdot P(C) \cdot P(D) \cdot P(C) \\
&= \frac{1}{5} \cdot \frac{1}{5}\cdot \frac{1}{5}\cdot \frac{1}{5} \\
\Rightarrow &P(A – C – D – C) = \frac{1}{625} \end{align}
Man kommt hier auch komplett ums Rechnen rum, wenn man seinen Kopf einschaltet. Die Melodie ist genau eine Auswahlmöglichkeit aus allen Kombinationen die es gilt.
Es gibt 625 Möglichkeiten, das weißt du aus A. Weil alle Kombinationen die gleiche Wahrscheinlichkeit haben, muss gelten:
\( P = \frac{1}{625}\)
Hier geht es zur allgemeinen Erklärung:

Lösung zu A3.3
Überlege dir, wieviele richtige Melodien es gibt und wie groß die Chancen auf die Melodien jeweils sind. Addiere diese dann.
Ob viermal C, D, E, G oder A gespielt wird, ist egal. Die Chance ist für jeden einzelnen gleich. Du kannst also z.B. P(A – A – A – A) ausrechnen und dann mal 5 nehmen.
\begin{align} P(A – A – A – A) &= \frac{1}{5} \cdot \frac{1}{5}\cdot \frac{1}{5}\cdot \frac{1}{5} \\
&= \frac{1}{625} \\
P_{ges} &= 5 \cdot \frac{1}{625} = \frac{5}{625} \end{align}
Auch hier kommt man mit Köpfchen weiter. Es gibt genau 5 richtige Melodien, die die Vorgabe erfüllen und alle haben dieselbe Chance. 5 von 625 ist die also die richtige Antwort.
Hier geht es zur allgemeinen Erklärung:
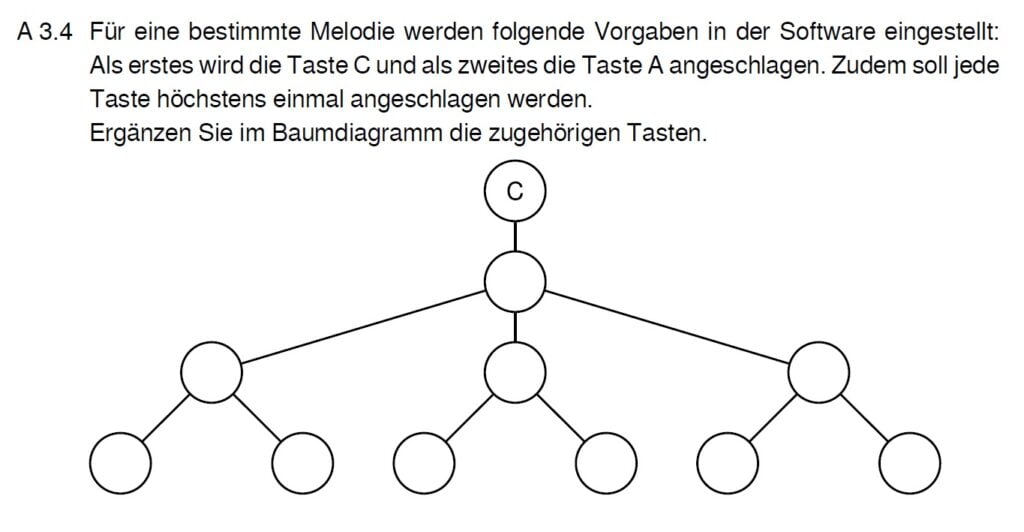
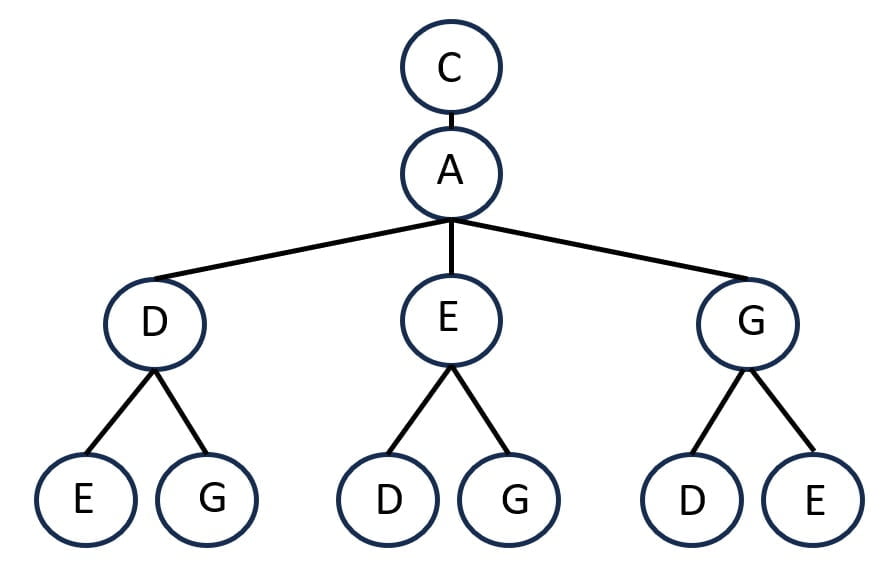
Lösung zu A3.4
Töne sollen nicht doppelt auftreten. Überprüfe immer mal wieder deine Äste.