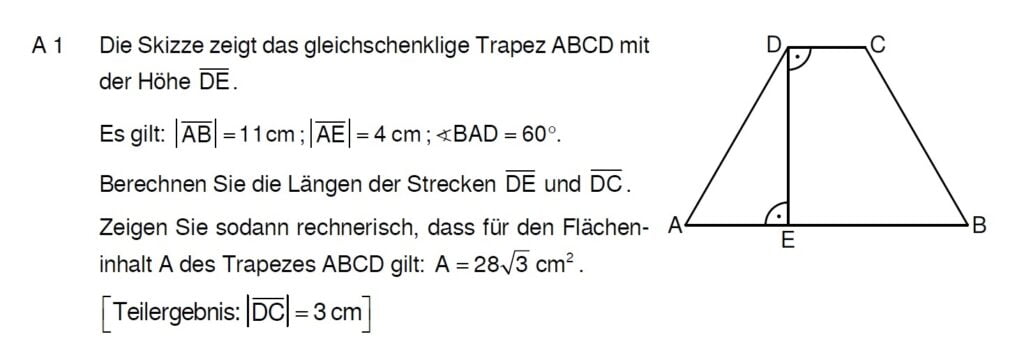
Lösung zu A1
Das Trapez ist gleichschenklig, damit kannst du leicht \(\overline{DC}\) ausrechnen.
Es ist ein Winkel gegeben und dir fehlt die Höhe. Du wirst die Sin/Cos/Tan-Tabelle aus der Formelsammlung brauchen.
Weil das Trapez gleichschenklig ist, haben die beiden „Flügel“ die gleiche Breite. Wenn du diese also 2mal von \( |\overline{AB}|\) abziehst, bekommst du \( |\overline{DC}|\)
\( |\overline{DE}|\) kannst du mit dem Tangens berechnen und dann in die Flächenformel einsetzen.
\begin{align}
|\overline{DC}| &= |\overline{AB}| – 2 \cdot |\overline{AE}| \\
&= 11 – 2 \cdot 4 = 3 cm \\
\\
&|\overline{DE}| \text{ mit dem Tangens}\\
tan(\angle BAD) &= \frac{|\overline{DE}|}{|\overline{AE}|}\\
tan(60°) &= \frac{|\overline{DE}|}{4} \,\,\, |\cdot 4 \\
|\overline{DE}| &= tan(60°) \cdot 4 \,\,\, \text{ mit } tan(60°) = \sqrt{3}\\
&= \sqrt{3} \cdot 4 cm \\
\\
&\text{Einsetzen in die Flächenformel:}\\
A &= 0,5 \cdot (|\overline{DC}| + |\overline{AB}|) \cdot |\overline{DE}|\\
&= 0,5 \cdot ( 11 + 3 ) \cdot \sqrt{3} \cdot 4 \\
&= 7 \cdot \sqrt{3} \cdot 4 \\
\Rightarrow &A = 28 \cdot \sqrt{3} cm^2 \end{align}
