

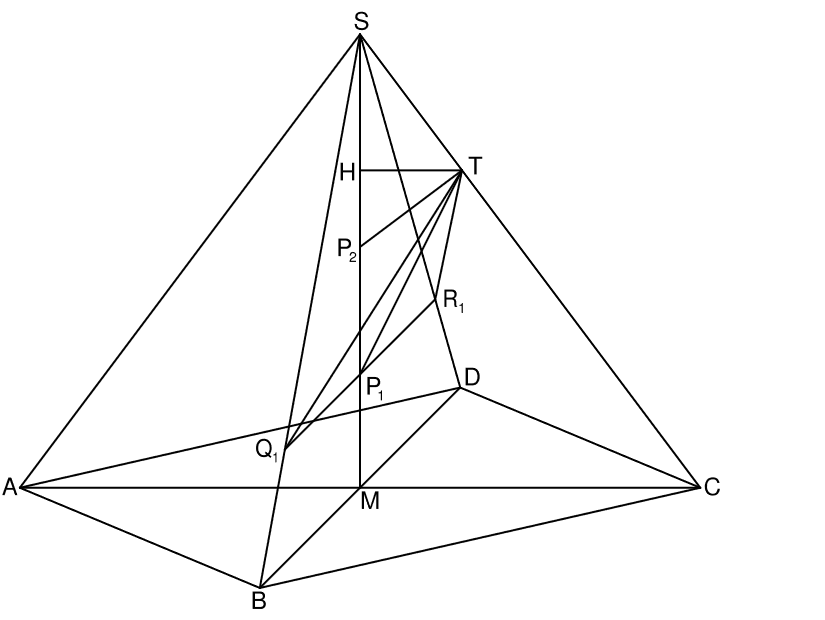
Lösung zu 2.1
Achte darauf, dass die Strecke von B zu D die richtige Länge hat!
\begin{align} &\text{Berechnung von } |\overline{CS}| \text{ mit dem Satz des Pythagoras:}\\
|\overline{CS}|^2 &= |\overline{MC}|^2 + |\overline{MS}|^2 \\
&= 6^2 + 8^2 \,\,\, |\sqrt{} \\
\Rightarrow &|\overline{CS}| = 10 cm \\
\\
&\angle MSC \text{ mit dem Tangens:}\\
tan(\angle MSC) &= \frac{|\overline{CM}|}{|\overline{MS}|}\\
&= \frac{6}{8} \,\,\, |tan^{-1}\\
\Rightarrow &\angle MCS = 36,87° \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.2
Für den Winkel benötigst du die Länge der Strecke \( |\overline{TP_1}| \)
Zeichnung siehe B2.1
Weil du keine Höhe im Dreieck kennst, ist die Sinusformel mit dem Winkel MCS ein guter Ansatz. Im Text verstecken sich die Längen für die anliegenden Seiten und wir können direkt rechnen:
\begin{align} A_{TSP_1} &= 0,5 \cdot |\overline{SP_1}| \cdot |\overline{ST}| \cdot sin(\angle MSC) \\
&= 0,5 \cdot (8 – 2) \cdot 3 \cdot sin(36,87°) \\
\Rightarrow &A_{TSP_1} = 5,40 cm^2 \end{align}
Das war der einfache Teil, kommen wir zum schwierigen. Im Dreieck TPS hast du zwar drei Angaben, kannst aber nicht direkt den gesuchten Winkel bestimmen.
Zuerst rechnet man mit dem Cosinussatz die Länge der Strecke \( \overline {P_1 T} \), um dann genug Angaben zur Berechnung des Winkels zu haben.
\begin{align} &\text{Berechnung von } |\overline{TP_1}| \text{ mit dem Cosinussatz:}\\
|\overline{TP_1}|^2 &= |\overline{SP_1}|^2 + |\overline{ST}|^2 – 2 \cdot |\overline{ST}| \cdot |\overline{SP_1}| \cdot cos(\angle MST) \\
&= 6^2 + 3^2 – 2 \cdot 6 \cdot 3 \cdot cos(36,87°)\,\,\, |\sqrt{}\\
\Rightarrow &|\overline{TP_1}| = 4,02 cm \\
\\
&\text{Berechnung von } \angle TP_1S \text{ mit dem umgeformten Cosinussatz:}\\
cos(\angle TP_1S) &= \frac{|\overline{TP_1}|^2 + |\overline{SP_1}|^2 – |\overline{ST}|^2}{2 \cdot |\overline{TP_1}| \cdot |\overline{SP_1}|}\\
&= \frac{4,02^2 + 6^2 – 3^2}{2 \cdot 4,02 \cdot 6 } \,\,\, |cos^{-1} \\
\Rightarrow &\angle TP_1S = 26,53° \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.3
Suche dir zur Berechnung ein rechtwinkliges Dreieck und überlege dir genau, wo der rechte Winkel ist.
Zeichnung siehe B2.1
Um den Wert für x zu berechnen, verwendest du für die Länge der Strecke \( \overline{SP_n} \) den Term in Abhängigkeit von x.
ACHTUNG: Der rechte Winkel ist bei T auf der Seitenkante, NICHT auf der Höhe bei P!
\begin{align} cos{\angle MSC} &= \frac{|\overline{ST}|}{|\overline{SP_2}|} \\
cos(36,87°) &= \frac{3}{8 – x} \,\,\, |\cdot (8 – x) \\
0,80 \cdot (8 – x) &= 3 \\
6,4 – 0,8x &= 3\,\,\, | – 6,4
-0,8x &= -3,4 \,\,\, |:(-0,8)
x &= 4,25 \end{align}
Im Video findest du noch eine andere Möglichkeit die Gleichung zu lösen.
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.4
Nutze die Parallelität und dein Geodreieck zum Einzeichnen. Achte darauf, alle Kanten der neuen Pyramide einzuzeichnen.
Zeichnung siehe B2.1
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.5
Hier ist erstmal genaues Hinsehen angesagt: Die Pyramide QRST hat die Grundfläche QRS und die Höhe HT. Sie liegt „schräg“ in der größen Pyramide.
Zur Berechnung des Pyramidenvolumens musst du also die Grundfläche (das Dreieck QRS) in Abhängigkeit von x und die Höhe bestimmen.
Für Die Grundfläche benötigst du die Streckenlänge \( |\overline{Q_n R_n}| \). Und weil diese parallel zu \( \overline{CD} \) liegt, funktionert das mit dem Vierstreckensatz:
\begin{align} &|\overline{Q_nR_n}| \text{ mit dem Vierstreckensatz:}\\
\frac{ |\overline{Q_n R_n}| }{ |\overline{BD}| } &= \frac{|\overline{SP_n}|}{|\overline{SM}|} \\
\frac{|\overline{Q_n R_n}|}{10} &= \frac{8 – x} {8} \,\,\, |\cdot 10 \\
|\overline{Q_n R_n}| &= \frac{80 – 10x} {8} \\
\Rightarrow & |\overline{Q_n R_n}| = (10 – 1,25x) cm \\
\\
&|\overline{HT}| \text{ mit dem Vierstreckensatz:}\\
\frac{|\overline{HT}|}{|\overline{CM}|} &= \frac{|\overline{ST}|}{|\overline{SC}|} \\
\frac{|\overline{HT}|}{6} &= \frac{3}{10} \,\,\, |\cdot 6 \\
\Rightarrow &|\overline{HT}| = 1,8 cm \\
\\
&\text{Einsetzen in die Flächenformel:}\\
V &= \frac{1}{3} \cdot A_g \cdot h \\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot |\overline{Q_n R_n}| \cdot |\overline{SP_n}| \cdot |\overline{HT}|\\
&= \frac{1}{3} \cdot \frac{1}{2} \cdot (10 – 1,25x) \cdot (8 – x) \cdot 1,8 \\
&= 0,3 \cdot (10 – 1,25x) \cdot (8 – x) \\
&= 0,3 (80 – 10x – 10x + 1,25x^2) \\
&= 0,3 (1,25x^2 – 20x + 80) \\
\Rightarrow &V(x) = (0,375x^2 -6x + 24) cm^3 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu B2.6
Achtung Falle! Welchen Öffnungsfaktor hat der Term in 2.5? Gibt es ein Maximum oder ein Minimum? Es ist Nachdenken angesagt!
Der Volumenterm hat einen postivien Öffnungsfaktor, also gibt ein Minimum, kein Maximum! Der Weg über den Taschenrechner funktionert hier nicht.
Durch die Veränderungen an der Pyramide wird das Volumen immer kleiner. Darum hat die unveränderte Pyramide das maximal mögliche Volumen. Die richtige x-Wert ist also x=0. Eingesetzt in den Volumenterm ergibt sich:
\( V(0) = 0,375 \cdot 0^2 -6 \cdot 0 +24 = 24 cm^3 \)
