2022 Haupttermin B1: Quadratische Funktionen

\begin{align} &\text{Einsetzen in die Scheitelform:}\\
y &= a \cdot (x – x_s)^2 + y_s \text{ mit S(3|5) und } a=-0,5\\
&= -0,5 \cdot (x – 3)^2 + 5 \\
&= -0,5 \cdot (x^2 – 6x + 9) + 5 \\
&= -0,5x^2 + 3x – 4,5 + 5 \\
\Rightarrow &y = -0,5x^2 +3x + 0,5 \end{align}

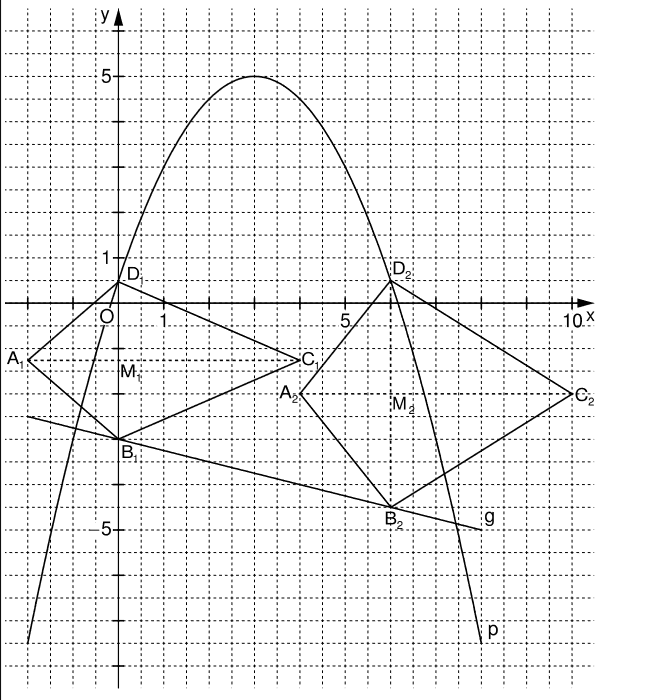
Zeichnung in B1.1

Um zu zeigen, dass der Flächeninhalt der Dreiecke ABD stets halb so groß wie der Flächeninhalt der Dreiecke BCD, betrachtest du die Formel \( A = 0,5 \cdot g \cdot h \).
Beide Dreiecke haben die Grundseite \(|\overline{BD}|\) und diese ist dementsprechend bei beiden gleich.
In 12 steht, dass \( |\overline{MA}| = 2 \text{ und } |\overline{MC}| = 4 \) gilt.
Die Höhe von BCD ist also doppelt so groß wie die Höhe von ABD. Das gilt immer.
Also ist auch der Flächeninhalt immer doppelt so groß.

Alle Werte für x sind erlaubt, solange diese zwischen den Schnittpunkten der Funktionen liegen. Um diese zu berechnen, setzt du die Funktionsterme gleich.
\begin{align} &\text{ Gleichsetzen der Funktionsterme:}\\
y_g &= y_p \\
-0,25x – 3 &= -0,5x^2 +3x + 0,5 \,\,\, |+0,25x + 3 \\
0 & = -0,5x^2 + 3,25x + 3,5 \\
\Rightarrow &GTR \, Mode \, A \\
x_1 &= 7,44 \lor x_2 = -0,94 \\
\Rightarrow &x \in ]-0,94 ; 7,44 [ \end{align}

Für den funktionalen Flächeninhalt \( A = 0,5 \cdot e \cdot f \) benötigst du die Streckenlänge \( |\overline{B_n D_n}(x)| \). Weil B und D die selbe Abszisse haben, rechnest du „oben – unten“:
\begin{align} &|\overline{B_n D_n}(x)| \text{durch „oben – unten“:}\\
|\overline{B_n D_n}(x)| &= y_D – y_b \\
&= -0,5x^2 + 3x + 0,5 – (-0,25x – 3) \\
&= -0,5x^2 + 3x + 0,5 + 0,25x + 3) \\
\Rightarrow &|\overline{B_n D_n}(x)|= -0,5x^2 + 3,25x +3,5 \\
\\
&\text{Einsetzen in die Flächenformel:}\\
A &= 0,5 \cdot |\overline{B_n D_n}(x)| \cdot |\overline{AC}|\\
&= 0,5 \cdot (-0,5x^2 + 3,25x +3,5) \cdot (2 + 4) \\
&= 0,5 \cdot (2 + 4) \cdot (-0,5x^2 + 3,25x +3,5) \\
&= 0,5 \cdot 6 \cdot (-0,5x^2 + 3,25x +3,5) \\
&= 3 \cdot (-0,5x^2 + 3,25x +3,5) \\
\Rightarrow A&= -1,5x² + 9,75x + 10,5 \\
\\
\Rightarrow &GTR \, Mode \, A \\
\Rightarrow &A_{max} = 26,34 cm² \text{ für } x = 3,25 \end{align}

Die beiden Schenkel \( |\overline{CM}| \text{und} |\overline{MD}| \) sind gleich groß, denn der 90° Winkel wird von der Symmetrieachse in zwei gleiche 45° Winkel zerteilt. Das ist nicht ganz einfach nachzuvollziehen. Mache dir einfach eine Skizze, dann wird es Klar.
\(|\overline{MC}|\) ist nach 1.2 4 cm lang. \(|\overline{BD}\) ist doppelt so lang wie \(|\overline{DM}|\), also \(2 \cdot 4 = 8 cm\).
Um die Koordinaten zu berechnen, setzt du die funktionale Streckenlänge mit 8 gleich.
\begin{align} |\overline{B_n D_n}(x)| &= 8 \\
-0,5x^2 + 3,25x +3,5 &= 8 \,\,\, |-8\\
-0,5x^2 + 3,25x – 4,5 &= 0 \\
\Rightarrow &GTR \, Mode \, A \\
x_1 &= 4,5 \lor x_2 = 2 \end{align}