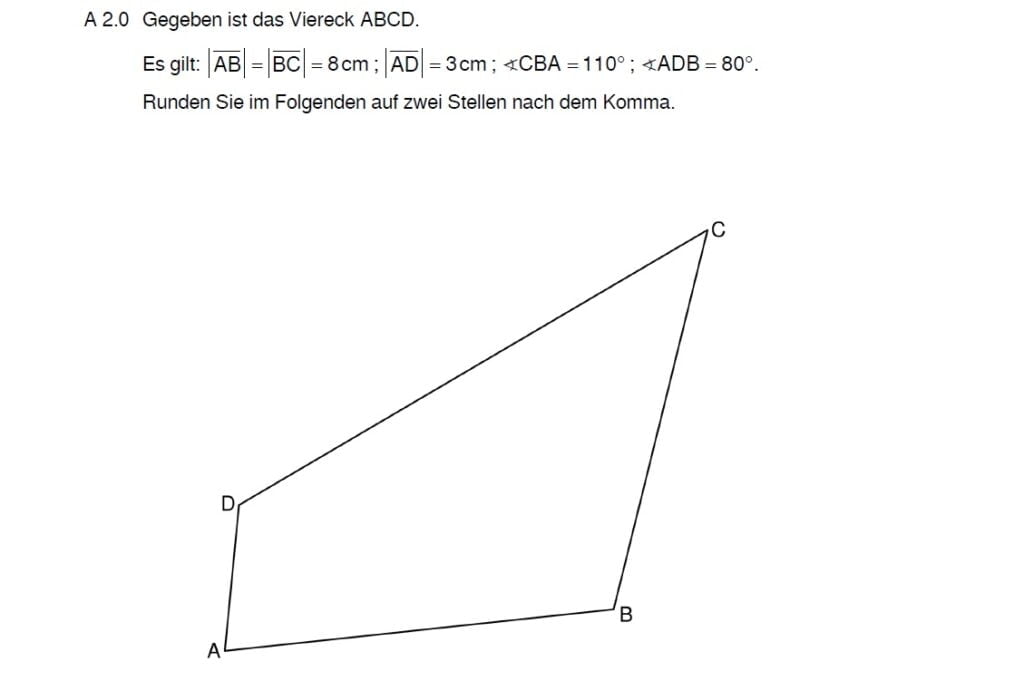

Lösung zu A2.1
Tipp 1: Berechne den Winkel im Dreieck ABD
Tipp 2: Für die Strecke fehlt dir eine Angabe. Die Innenwinkelsumme hilft dir weiter.
\begin{align}&\angle DBA \text{ mit dem Sinussatz:}\\
\frac{sin(\angle DBA)}{|\overline{AD}|} &= \frac{sin(\angle ADB)}{|\overline{AB}|}\\
\frac{sin(\angle DBA)}{3} &= \frac{sin(80°)}{8} \,\,\,|\cdot 3 \\
sin(\angle DBA)&= \frac{sin(80°)}{8} \cdot 3 \,\,\, |sin^{-1}\\
\Rightarrow &\angle DBA = 21,67° \end{align}
Um \( |\overline{BD}|\) zu berechnen, brauchst du den Winkel BAD. Diesen kannst du mit der Innenwinkelsumme des Dreiecks bestimmen.
\begin{align} &\angle BAD \text{ mit der Innenwinkelsumme:}\\
\angle BAD &= 180° – 80° – 21,67° = 78,33° \\
\\
&|\overline{BD}| \text{ mit dem Cosinussatz:}\\
|\overline{BD}|^2 &= |\overline{AB}|^2 + |\overline{AD}|^2 – 2 \cdot |\overline{AB}| \cdot |\overline{AD}| \cdot cos(\angle BAD) \\
&= 8^2 + 3^2 – 2 \cdot 8 \cdot 3 \cdot cos(78,33°)\\
\Rightarrow &|\overline{BD}|= 7,96 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu A2.2
Zerteile das Viereck in zwei Dreiecke. Am besten entlang einer Strecke, die du bereits ausgerechnet hast.
Weil das Viereck keine Regelmäßigkeit besitzt, musst du es in zwei Dreiecke zerteilen. Die Diagonalenlänge BD ist als Ersatzergebnis gegeben, also brauchst du sie wahrscheinlich.
Das Viereck wird in ABD und BCD zerteilt und deren Flächeninhalte mit der Sinus-Formel berechnet.
\begin{align} &A_{ABD} \text{ mit der Sinus-Formel:}\\
A_{ABD} & = 0,5 \cdot |\overline{AB}| \cdot |\overline{BD}| \cdot sin(\angle DBA) \\
&= 0,5 \cdot 8 \cdot 7,96 \cdot sin(21,67°) \\
\Rightarrow &A_{ABD}= 11,76 cm² \\
\\
&A_{BCD} \text{ mit der Sinusformel:}\\
A_{BCD} & = 0,5 \cdot |\overline{BD}| \cdot |\overline{BC}| \cdot sin(\angle CBD) \\
&= 0,5 \cdot 7,96 \cdot 8 \cdot sin(110° – 21,67°) \\
\Rightarrow &A_{ABD}= 31,83 cm² \\
\\
A_{ges} &= 11,76 + 31,83 = 43,59 cm^2 \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu A2.3
Zeichne zuerst den Mittelpunkt ein und suche dann im Text nach dem Radius.
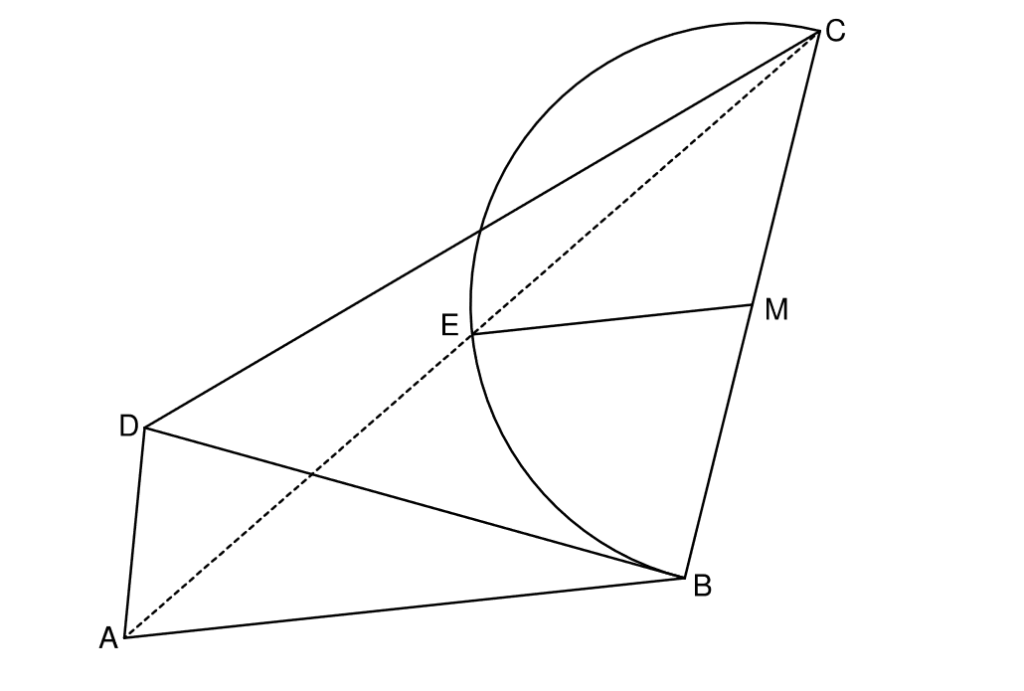
Hier geht es zur allgemeinen Erklärung:

Lösung zu A2.4
Im ersten Satz der Aufgabe steht eine Eigenschaft. Was kannst du daraus für die Winkel schließen?
Weil EM zu AB parallel ist, ist ABME ein Trapez. Damit gilt:
\begin{align} \angle MBA + \angle EMB &= 180° \text{ Ergänzungswinkel} \\ 110° + \angle EMB &= 180° \\ \angle EMB &= 70° \\ \\ &\text{Berechnung der Bogenlänge b:}\\ b &= \frac{\angle EMB}{360°} \cdot 2 \cdot |\overline{MC}| \cdot \pi \\ &= \frac{70°}{360°} \cdot 2 \cdot 4 \cdot \pi \\ \Rightarrow &b = 4,89 cm \end{align}
Hier geht es zur allgemeinen Erklärung:

Lösung zu A2.5
Prozentrechnung: Anteil / Ganzes * 100%
\begin{align} A \text{ mit der Sektorformel:}\\
A &= \frac{\angle EMB}{360°} \cdot |\overline{MC}|^2 \cdot \pi \\
&= \frac{70°}{360°} \cdot 4^2 \cdot \pi\\
\Rightarrow &A = 9,77 cm^2 \\
\\
&p \text{ mit der Prozentformel:}\\
p &= \frac{Anteil}{Gesamt} \cdot 100 \% \\
&= \frac{9,77}{43,58} \cdot 100 \% \\
\Rightarrow &p = 22,42 \% \end{align}
