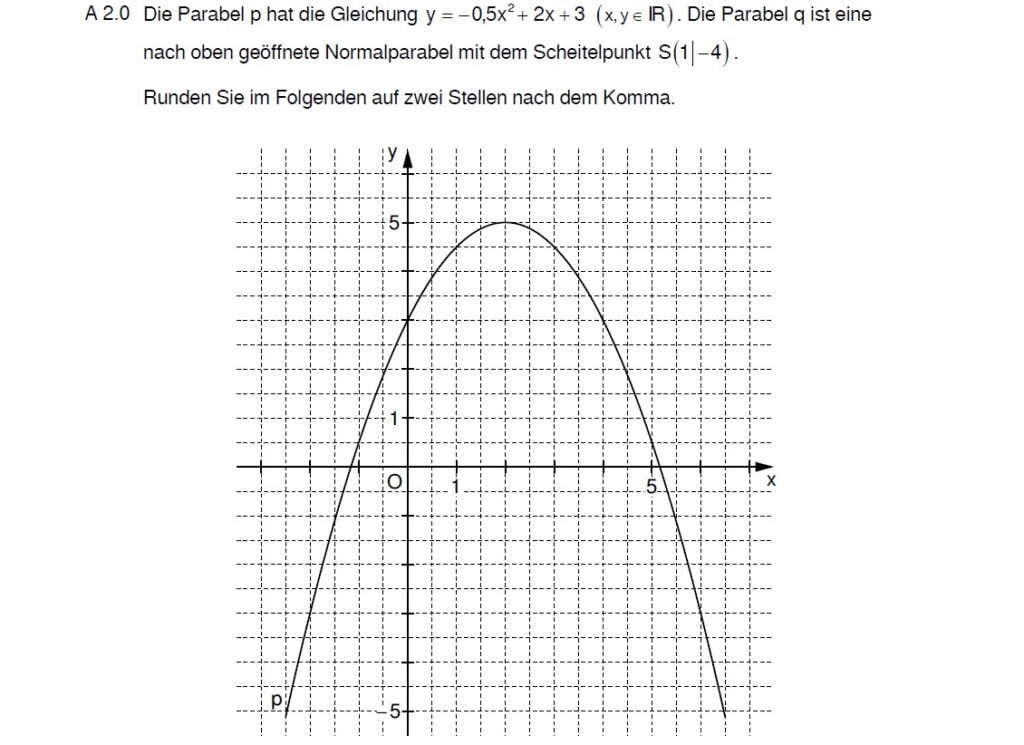

Lösung zu 2.1
In der Aufgabe ist der Scheitelpunkt geben, also arbeitest du mit der Scheitelform.
Weil es sich um eine nach oben geöffnete Normalparabel handeln, weißt du, dass der Öffnugsfaktor \( a = 1 \) ist.
\begin{align}
y & = a \cdot ( x – x_s)^2 + y_s \,\,\, \text{mit } S(1|-4)\\
&= (x – 1)^2 – 4 \\
&= x^2 – 2x + 1 – 4 \\
\Rightarrow &y = x^2 -2x -3 \end{align}
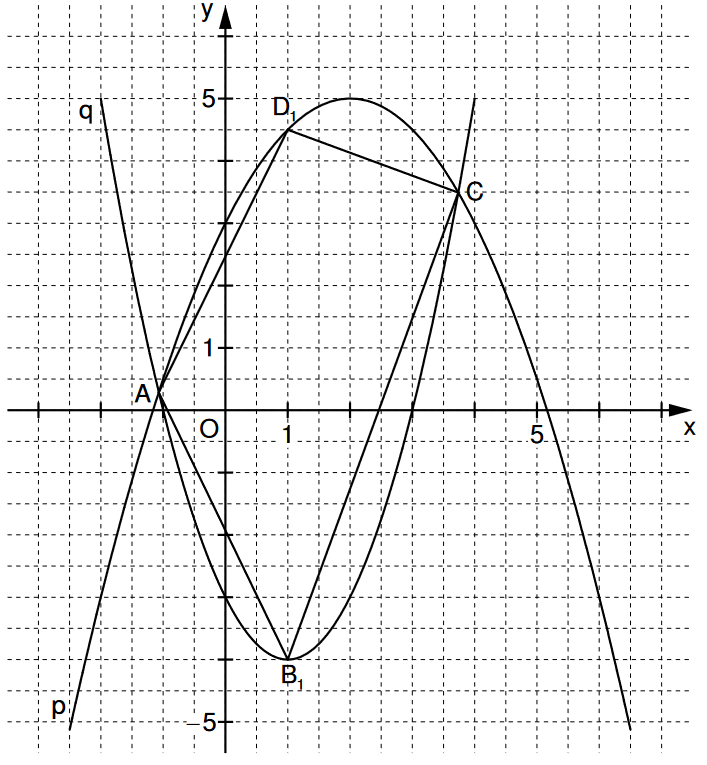
Zurück zum MAP-Hack:

Lösungen zu 2.2
Benutzte das Vorgehen aus „Intervallgrenzen bestimmen“. Setze die Funktionsterme gleich und löse die Gleichung für x. Setzte das x in die Fenktionsgleichung ein, um die y-Koordinate zu berechnen.
\begin{align} &\text{Gleichsetzen der Funktionsterme:}\\
y_q &= y_p \\
x^2 -2x – 3 &= -0,5x^2 +2x +3 \,\,\, |+0,5x^2 -2x -3 \\
1,5x^2 -4x -6 &= 0 \\
\Rightarrow >R \\
\Rightarrow x&= -1,07 \,\, \lor \,\, x=3,74 \\
\\
&\text{Einsetzen in die allgemeinen Koordinaten:}\\
A(x|x^2 -2x -3) &\rightarrow A(-1,07|(-1,07)^2 -2 \cdot (-1,07) -3) \\
\Rightarrow A(-1,07|0,28)\\
\\
C(x|x^2 -2 \cdot x -3) &\rightarrow C(3,74|3,74^2 -2 \cdot 3,74 -3) \\
\Rightarrow C(3,74|3,51) \end{align}
Zurück zum MAP-Hack:

Lösung zu 2.3
Suche die passende Stelle an der x-Achse und zeichne die Punkt auf den Funktionen ein. Dann musst du nurnoch verbinden.
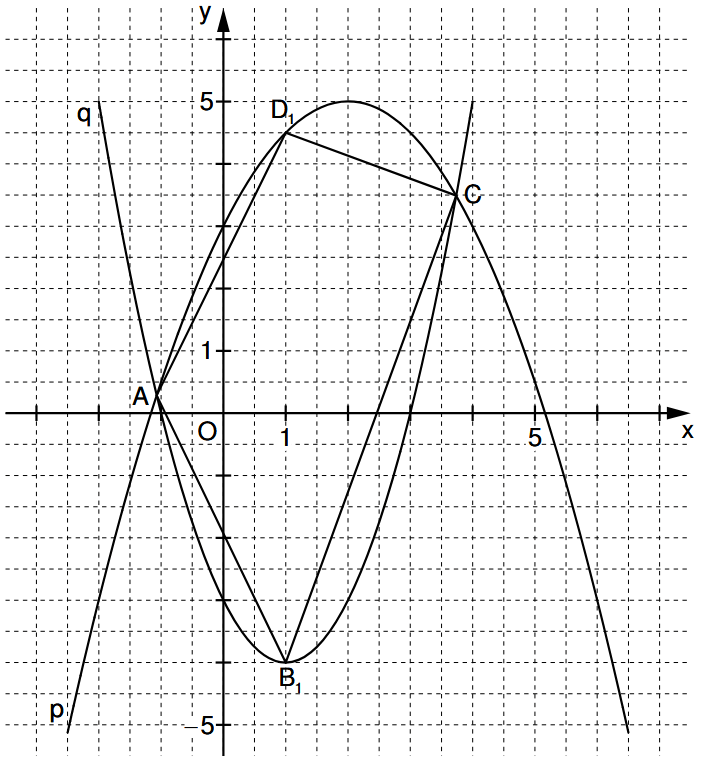
Zurück zum MAP-Hack:

Lösungen zu 2.4
Welche Eigenschaften hat ein Trapez? Welche davon kanst du im Koordinatensystem einfach berechnen?
(Spoiler: Es ist die Steigung)
Dass es sich um ein Trapez handelt, müssen zwei gegenüberliegende Seiten – hier AD und BC – parallel sein.
Im Koordinatensystem kannst du Parallelität überprüfen, indem du die Steigungen der beiden Geraden vergleichst.
Die Idee der Lösung ist also: Bestimme die beiden Steigungen von AD und BC aus den Koordinaten und wenn diese gleich sind, ist es ein Trapez.
Die Koordinaten von A und C kennst du aus 2.2 und B liegt hier auf dem Scheitel S. B hat also die selben Koordinaten wie S.
Bleibt nurnoch D zu berechnen.
\begin{align} &\text{Berechnung der Koordinaten von } D_1 :\\
D_1 &(x|-0,5 \cdot x^2 +2x+ 3 ) \rightarrow D_1 (1|-0,5 \cdot 1^2 + 2 \cdot 1 + 3) \\
\Rightarrow &D_1(1|4,5) \,\,\,\, B_1(1|-4) \, ; \, A(-1,07|0,28) \, ; \, C(3,74|3,51) \\
\\
&\text{Berechnung der Steigungen aus den Koordinaten:}\\
\text{Allgemein:} m &= \frac{y_2 – y_1}{x_2 – x_1}\\
\\
m_{AD_1} &= \frac{y_D – y_A}{x_D – x_A}\\
&= \frac{ 4,5 – 0,28}{1-(-1,07)} \\
\Rightarrow &m_{AD_1} = 2,04 \\
\\
m_{BC} &= \frac{y_C – y_B}{x_C – x_B} \\
&= \frac{3,51 – (-4)}{3,74 – 1} \\
\Rightarrow &m_{BC} = 2,74 \end{align}
Die beiden Steigungen sind nicht gleich, also ist das Viereck kein Trapez
