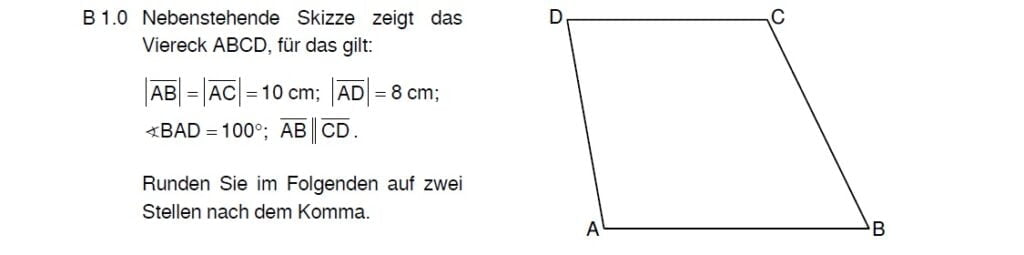

Lösung zu 1.1
Im rechtwinkligen Dreieck hast du Sin/Cos/Tan und SdP zur Auswahl. Gibt es keinen rechten Winkel, bleibt nur noch Sinussatz und Cosinussatz.
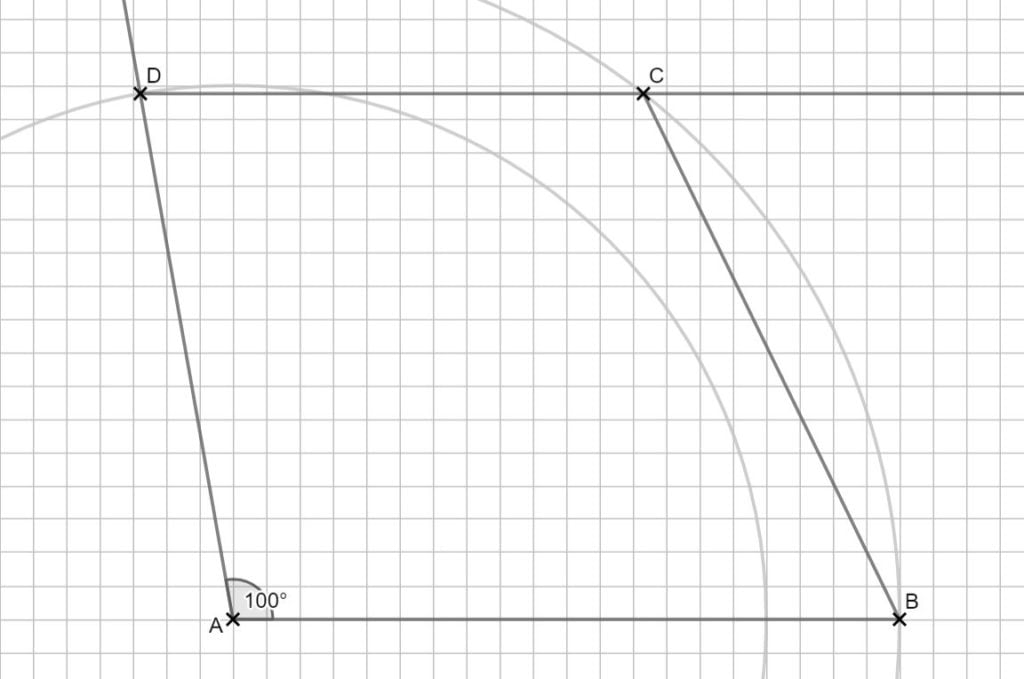
Achtung, nicht wie ich die Diagonalen vergessen 😉
\begin{align} & \overline{BD} \text{ mit dem Cosinus-Satz:} \\
|\overline{BD}|^2 &= |\overline{AB}|^2 + |\overline{AD}|^2 – 2 \cdot |\overline{AB}| \cdot |\overline{AD}| \cdot cos(\angle BAD) \\
&= 10^2 + 8^2 – 2 \cdot 10 \cdot 8 \cdot cos(100°) \\
\Rightarrow & |\overline{BD}| = 13,85 cm \\
\\
& \angle DBA \text{ mit Sinus-Satz:} \\
\frac{sin(\angle DBA)}{|\overline{AD}|} &= \frac{sin(\angle BAD)}{|\overline{BD}|} \\
\\
\frac{sin(\angle DBA)}{8} &= \frac{sin(100°)}{13,85} \, \, | \cdot 8 \\
sin(\angle DBA) &= \frac{sin(100°)}{13,85} \cdot 8 \\
\Rightarrow \angle DBA &= 34,67° \end{align}
Zurück zum MAP-Hack:

Lösung zu 1.2
Zeit für besondere Winkelbeziehungen – Stoff der 7. Klasse. Wechsel-, Stufen- oder Ergänzungswinkel. Was war das denn nochmal?
\begin{align} & \angle DCA \text{ mit dem Sinussatz:} \\
\frac{sin(\angle DCA)}{|\overline{AD}|} &= \frac{sin(180° – 100°)}{|\overline{AC}|} \\
\frac{sin(\angle DCA)}{8} &= \frac{sin(80°)}{10} \, \, |\cdot 8 \\
sin(\angle DCA) &= \frac{sin(80°)}{10} \cdot 8 \\
\Rightarrow &\angle DCA = 51,98° \end{align}
Weil AB und CD parallel zueinander sind, sind die Winkel BAC und DCA Wechselwinkel und deshalb gleich groß. In mathematischen Bezeichnungen:
\( AB || CD \Rightarrow \angle BAC = \angle DCA = 51,98° (\text{Wechselwinkel}) \)
Lösung zu 1.3
Das Viereck setzt sich aus den Dreiecken \(\triangle ABC \) und \(\triangle ACD \) zusammen. Du berechnest die Flächeninhalte der einzelnen Dreiecke und addierst anschließend.
\begin{align} A_{\triangle ABC} &= 0,5 \cdot |\overline{AB}| \cdot |\overline{AC}| \cdot sin(\angle BAC) \\
&= 0,5 \cdot 10 \cdot 10 \cdot sin(51,98°) \\
\Rightarrow &A_{\triangle ABC} = 39,39 cm^2 \\
\\
A_{\triangle ACD} &= 0,5 \cdot \overline{AC} \cdot \overline{AD} \cdot sin(\angle CAD) \\
&\angle CAD = \angle BAD – \angle BAC = 100° – 51,98° \\
& \Rightarrow \angle CAD = 48,02° \\
A_{\triangle ACD} &= 0,5 \cdot 10 \cdot 8 \cdot sin(48,02°) \\
\Rightarrow &A_{\triangle ACD} = 29,74 cm^2 \\
\\
A_{ABCD} &= A_{\triangle ABC} + A_{\triangle ACD} \\
&= 39,39 + 29,74 \\
\Rightarrow &A_{ABCD} = 69,13 cm^2 \end{align}
Zurück zum MAP-Hack:

Lösung zu 1.4
Im Berührpunkt steht der Radius senkrecht auf die Strecke. So findest du den Punkt E mit deinem Geodreieck.

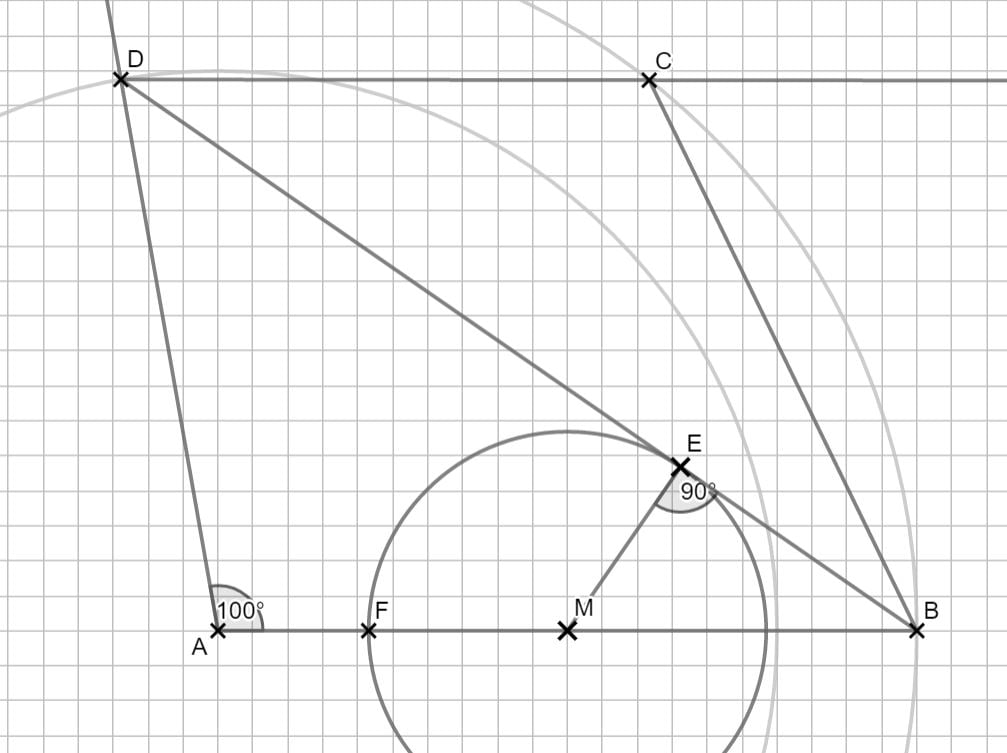
Zurück zum MAP-Hack:

Lösung zu 1.5
Die gesuchte Fläche setzt sich aus den Flächen des Kreissektors, der durch E und F begrenzt ist, und dem Dreieck BEM zusammen. Weil der Kreis in E die Strecke berührt, ist dort ein rechter Winkel.
Um den Flächeninhalt des Dreiecks zu berechnen benötigst du die Länge der Strecke \(\overline{ME}\):
\begin{align} &A_{\triangle BEM} \text{ über} |\overline{ME}|: \\
sin(\angle EBM) &= \frac{|\overline{ME}|}{|\overline{BM}|} \, \, |\cdot |\overline{BM}| \\
|\overline{ME}| &= sin(\angle EBM) \cdot |\overline{BM}| \\ &= sin(34,67°) \cdot 5 = 2,84 cm \\
\\
\angle BME &= 180° – \angle MEB – \angle EBM \,\,\, (\text{Innenwinkelsumme}) \\
&= 180° – 90° – 34,67° \\
\Rightarrow & \angle BME = 55,33° \\
\\
A_{\triangle BEM} &= 0,5 \cdot |\overline{MB}| \cdot |\overline{ME}| \cdot sin(\angle BME) \\
&= 0,5 \cdot 5 \cdot 2,84 \cdot sin(55,33°) \\
\Rightarrow &A_{\triangle BEM} = 5,84 cm^2 \end{align}
Um den Flächeninhalt des Kreissektors zu berechnen, benötigst du den Winkel BME:
\begin{align} A_{Sektor} &= \frac{\angle EMF}{360°} \cdot |\overline{ME}|^2 \cdot \pi \\
\\
\angle EMF &= 180° – \angle BME \,\,\, (\text{Ergänzungswinkel}) \\
&= 180° – 55,33° \\
\Rightarrow \angle EMF &= 124,67° \\
\\
A_{Sektor} &= \frac{124,67°}{360°} \cdot 2,84^2 \cdot \pi \\
\Rightarrow &A_{Sektor} = 8,77 cm^2 \\
A &= A_{\triangle BEM} + A_{Sektor} = 5,84 + 8,77 = 14,61 cm^2 \\
\\
&\text{Berechnung des Prozentsatzes:} \\
p &= \frac{A}{A_{ABCD}} \cdot 100 \% \\ &= \frac{14,61}{69,12} \cdot 100 \% = 21,14 \% \end{align}
Zurück zum MAP-Hack:

Lösung zu 1.6
Grundwissen aktivieren: https://map-hack.de/grundwissen/eigenschaften-des-abstandes/
\begin{align} &\angle CGD \text{ mit der Innenwinkelsumme:} \\ \angle CGD &= 180° – 51,98° – 34,67° = 93,35° \end{align}
Der Abstand d ist die kürzeste Verbindungsstrecke und steht immer senkrecht (90°). Weil der Winkel größer als 90° ist, ist die Länge Strecke DG auch größer als der Abstand.

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib’ hier und du bekommst eine Antwort!