2019 Nachtermin A2: Raumgeometrie

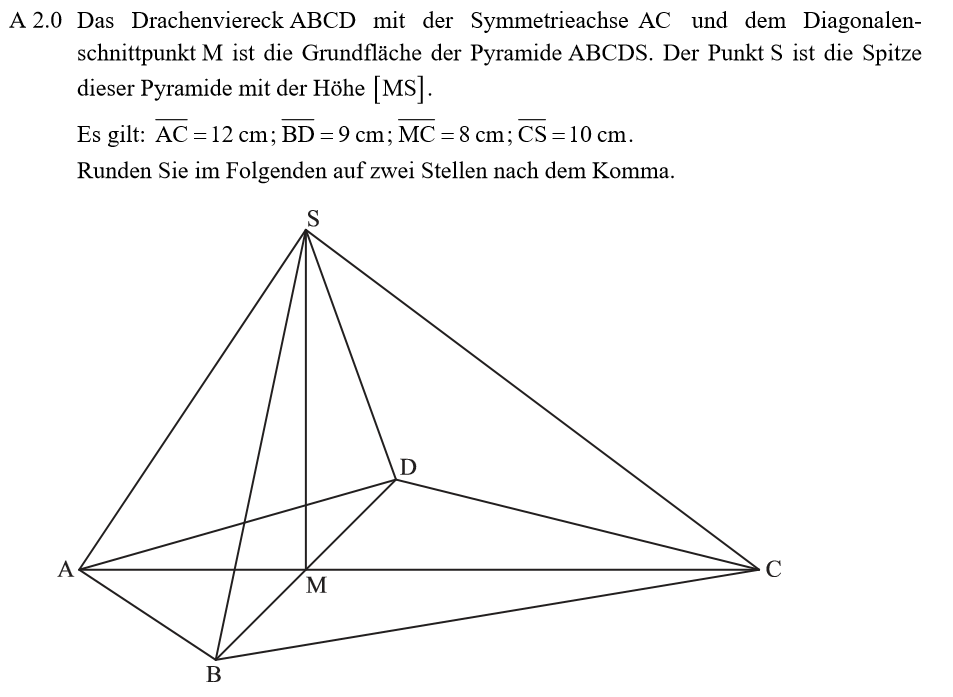
Um in die Volumenformel einsetzen zu können, benötigst du die Höhe \( h = \overline{MS} \). Die Grundfläche ist eine Raute, du kannst also die Formel A = 0,5 e f verwenden.

\begin{align} &\overline{MS} \, mit \, dem \, Satz \, des \, Pythagoras: \\ \overline{CS}^2 &= \overline{MS}^2 + \overline{CM}^2 \,\, | – \overline{CM}^2 \\ \overline{MS}^2 &= \overline{CS}^2 – \overline{MS}^2 = 10^2 – 8^2 \\ \Rightarrow &\overline{MS} = 6cm \\ \\ &Einsetzen \, in \, die \, Volumenformel: \\ V &= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{AC} \cdot \overline{BD} \cdot \overline{MS} \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot 12 \cdot 9 \cdot 6 \\ \Rightarrow &V = 108 cm^3 \end{align}

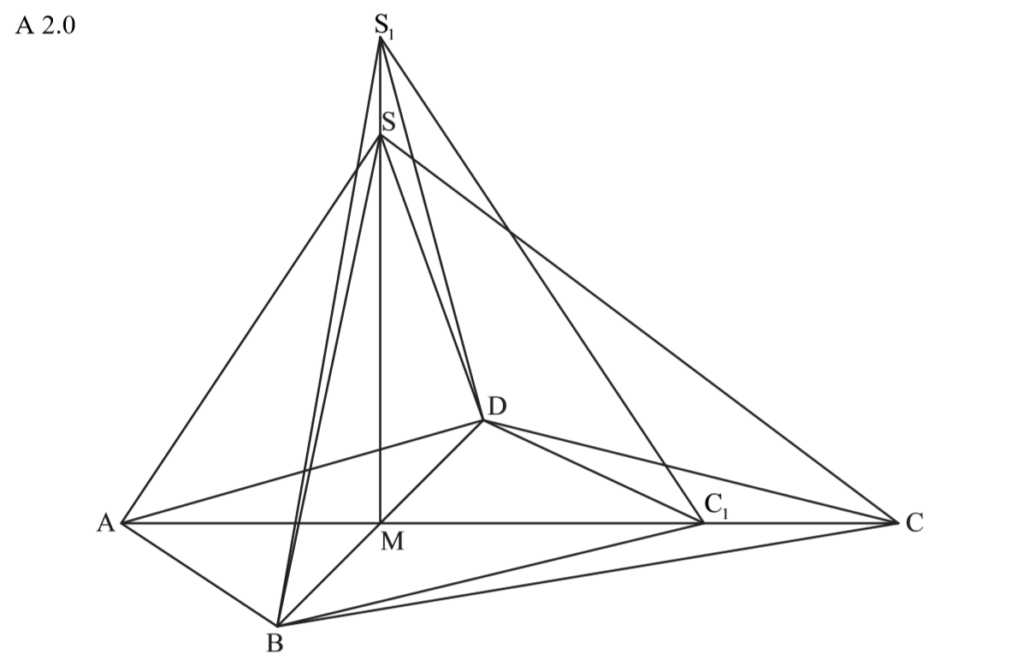
Zuerst überlegst du dir die funktionalen Streckenlängen, setzt sie dann in die Volumenformel ein und vereinfachst.

\begin{align} & \overline{MC_n}(x) = 8 – 2x \, \\ & \overline{MS_N}(x)=6 + x \\ V(x) &= \frac{1}{3} \cdot \frac{1}{2} \cdot \overline{MC_n}(x) \cdot \overline{BD} \cdot \overline{MS_n}(x) \\ &= \frac{1}{3} \cdot \frac{1}{2} \cdot (8-2x) \cdot 9 \cdot (6+x) \\ &=\frac{3}{2} \cdot (8-2x) \cdot (6+x) \\ &= \frac{3}{2} \cdot (48 + 8x – 12x – 2x^2) \\ &= \frac{3}{2} \cdot (-2x^2 -4 x + 48) \\ \Rightarrow &V(x) = (-3x^2 -6x +72) cm^3 \end{align}

Ist die neue Pyramide um 70% kleiner, entspricht ihr Volumen 30% der ursprünglichen Pyramide. Stelle eine gleichung auf und löse die Gleichung!

\begin{align} V(x) &= 0,3 \cdot 108 \\ -3x^2 -6x + 72 &= 32,4 \,\,\, |-32,4 \\ -3x^2 -6x +39,6 &= 0 \\ \Rightarrow &GTR: (x_1 = -4,77) \lor x_2 = 2,77 \end{align}

Der negative Wert entfällt, da x ein Wert zwischen 0 und 4 ist.

\begin{align} &Ansatz \, mit \, Tangens: \\
tan(\angle S_3 C_3 M) &= \frac{\overline{MS_3}}{\overline{MC_3}} \\
tan(72°) &= \frac{6+x}{8-2x} \,\,\, |\cdot (8-2x) \\
3,078 \cdot (8-2x) &= 6 +x \\
24,624 – 6,156x &= 6 + x \,\,\, +6,156x -6 \\
18,624 &= 7,156x \,\, \, |:7,154 \\
\Rightarrow &x= 2,60 \end{align}

Auch wenn der Mathe-Lehrer in mir weint, empfehle ich dir hier zuerst tan(72°) auszurechnen und mit einem gerundeten Ergebnis zu vereinfachen.