
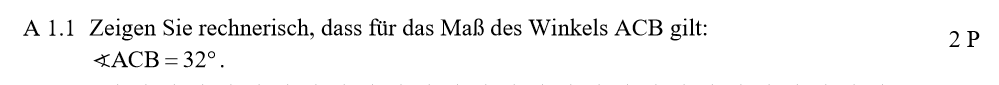
Lösungen zu A1.1
\begin{align} & \angle ACB \, mit \, dem \, umgeformten \, Cosinussatz: \\ \overline{AB}^2 &= \overline{AC}^2 + \overline{BC}^2 – 2 \cdot \overline{AC} \cdot \overline{BC} \cdot cos(\angle ACB) \\ cos(\angle ACB) &= \frac{\overline{AC}^2 + \overline{BC}^2 – \overline{AB}^2}{2 \cdot \overline{AC} \cdot \overline{BC}} \\&= \frac{150^2 + 75^2 – 95^2}{2 \cdot 150 \cdot 75} \\ \Rightarrow & \angle ACB = 32° \end{align}
Zurück zum MAP-Hack:
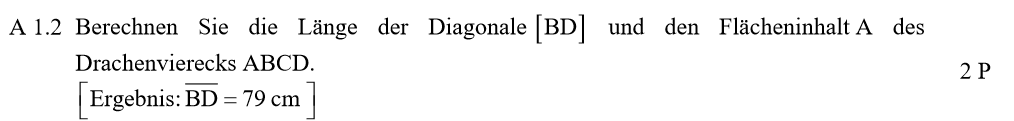
Lösungen zu A1.2
Zuerst musst du die Länge der Strecke [BD] berechnen. Das erkennst du schon daran, dass es als Ersatzergebnis gegeben ist.
\begin{align} &\overline{BD} \, mit \, dem \, Sinus: \\ sin(\angle ACB) &= \frac{0,5 \cdot \overline{BD}}{\overline{BC}} \\ sin(32°) &= \frac{0,5 \cdot \overline{BD}}{75} \,\,\, | : \frac{0,5}{75} \\ \overline{BD} &= sin(32°) : \frac{0,5}{75} \\ \Rightarrow &\overline{BD} = 79 cm \\ \\ &Berechnung \, des \, Flächeninhalts: \\ A_{Drache} &= 0,5 \cdot e \cdot f \\ &= 0,5 \cdot \overline{AC} \overline{BD} \\ &= 0,5 \cdot 150 \cdot 79 \\ \Rightarrow &A_{Drache} = 5925 cm^2 \end{align}

Lösung zu A1.3
In der Flächenformel der Raute erkennst du die wichigen Bestandteile, nämlich die Diagonalen [AC] und [BD]. [BD] verändert sich nicht, die Diagonale [AC] wird von 150 cm auf 100 cm gekürzt.Die Verkürzung sind 50 von 150, also ein Drittel oder auch näherungsweise 33%.

Du hast eine Frage zu einer Teilaufgabe oder zur Lösung? Schreib‘ hier und du bekommst eine Antwort!
Könnte man bei der A.1.2 nicht auch den Cosinussatz verwenden , um die Strecke BD herauszufinden ?
Ja, das funktioniert auch. Einfach den Ansatz verwenden, der dir besser gefällt.