Lösung zu A2.1
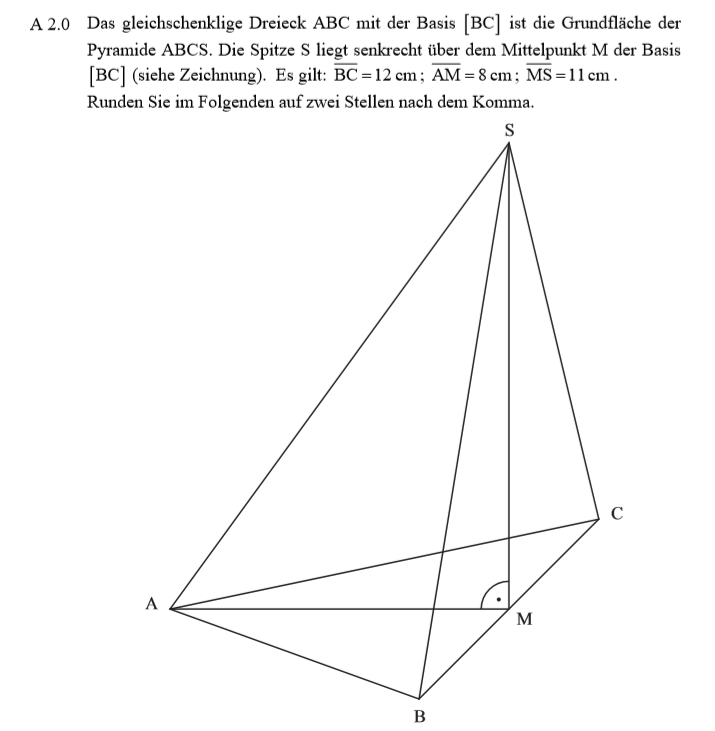
\begin{align} &\overline{AS} \, mit \, dem \, Satz \, des \, Pythagoras: \\
\overline{AS}^2 &= \overline{AM}^2 + \overline{MS}^2 \\
&= 8^2 + 11^2 \\
\Rightarrow &\overline{AS} = 13,60 cm \\
\\
&\varphi \, mit \, dem \, Tangens: \\ tan(\varphi) &= \frac{\overline{AM}}{\overline{MS}} \\ &= \frac{8}{11} \\ \Rightarrow &\varphi = 36,03° \end{align}
Zurück zum MAP-Hack:

Lösung zu A2.2
Zeichne die Strecke [PQ] ein
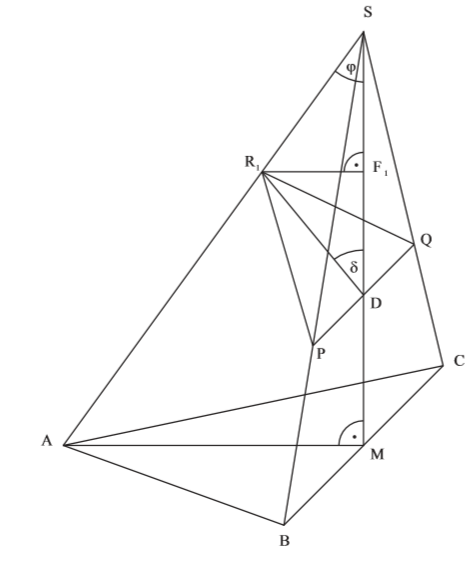
\begin{align} &\overline{PQ} \, mit \, dem \, Vierstreckensatz: \\ \frac{\overline{PQ}}{\overline{BC}} &= \frac{\overline{SD}}{\overline{SM}} \\ \\ mit & \overline{SD} = \overline{SM} – \overline{MD} \\ \\ \frac{\overline{PQ}}{\overline{BC}} &= \frac{\overline{SM} – \overline{MD}}{\overline{SM}} \, \, \, |\cdot \overline{BC} \\ \overline{PQ} &= \frac{\overline{SM} – \overline{MD}}{\overline{SM}} \cdot \overline{BC} \\ &= \frac{11-4}{11} \cdot 12 \\ \Rightarrow &\overline{PQ} = 7,64 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu A2.3
Um \(\delta \) berechnen zu können, musst du zuerst die länge der Strecke [DR] bestimmen.
\begin{align} &\overline{DR_1} \, mit \, dem \, Cosinussatz: \\
\overline{DR_1}^2 &= \overline{SD}^2 + \overline{SR}^2 – 2 \cdot \overline{SD} \cdot \overline{SR} \cdot cos(\varphi) \\
&= (11-4)^2 + (13,6 – 9)^2 – 2 \cdot 7 \cdot 4,6 \cdot cos(36,03°) \\
\Rightarrow &\overline{DR_1} = 4,25 cm \\ \\ &\delta \, mit \, dem \, Sinussatz: \\
\frac{sin(\delta)}{\overline{SR}} &= \frac{sin(\varphi)}{\overline{DR_1}} \,\,\, |\cdot \overline{SR} \\ sin(\delta) &= \frac{sin(\varphi)}{\overline{DR_1}} \cdot \overline{SR} \\ &= \frac{sin(36,03°)}{4,25} \cdot (13,60 – 9) \\ \Rightarrow &\delta = 39,54° \end{align}

Lösung zu A2.4
Weil die Höhe immer senkrecht steht, kann mit dem Sinus angesetz werden.
\begin{align} &\overline{R_n F_n} \, mit \, dem \, Sinus: \\ sin(\varphi) &= \frac{\overline{R_n F_n}}{\overline{AS} – x} \, \, \, |\cdot (\overline{AS} – x) \\ \overline{R_n F_n} &= sin(\varphi) \cdot (13,60 – x) \\ &= sin(36,03°) \cdot (13,60 – x) \\ \Rightarrow &\overline{R_n F_n} = (8,00 – 0,59x) cm \end{align}

Kann man bei A 2.3 den Winkel auch mit Kosinussatz berechnen weil bei mir kommt da dann 39,51° raus?
Ja, das klappt auch, denn du kennst ja drei Seiten im Dreieck. Die Abweichung in der zweiten Nachkommastelle kann an Rundung im Taschenrechner liegen.