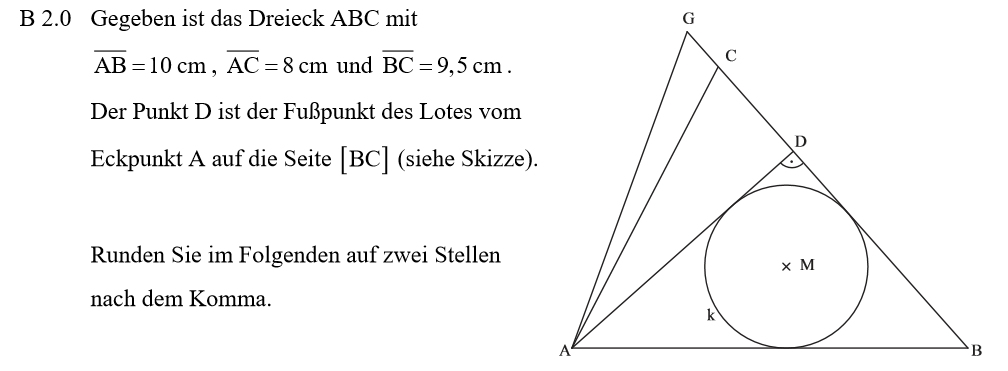
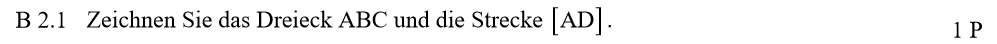
Lösung zu B2.1
Zurück zum MAP-Hack:
Lösung zu B2.2
\begin{align}& \beta\, mit \, dem \, umgeformten \, Cosinussatz: \\ \overline{AC}^2 &= \overline{AB}^2 + \overline{BC}^2 – 2 \cdot \overline{AB} \cdot \overline{BC} \cdot cos(\beta) \\ \cos(\beta) &= \frac{\overline{AB}^2 + \overline{Bc}^2 – \overline{AC}^2}{2 \cdot \overline{AB} \cdot \overline{BC}} \\ &= \frac{10^2 + 9,5^2 – 8^2}{2 \cdot 10 \cdot 9,5} \\ \Rightarrow &\beta = 48,36° \\ \\ &\varepsilon \, mit \, der \, Innenwinkelsumme: \\ \varepsilon &= 180° – 90° – \beta \\ &= 180° – 90° – 48,36° \\ \Rightarrow &\varepsilon = 41,64° \\ \\ & \overline{AD} \, mit \, dem \, Sinus: \\ sin(\beta) &= \frac{\overline{AD}}{\overline{AB}} \,\,\, |\cdot \overline{AB} \\ \overline{AD} &= \overline{AD} \cdot sin(\beta) \\ &= 10 \cdot sin(48,36°) \\ \Rightarrow &\overline{AD} = 7,47 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.3
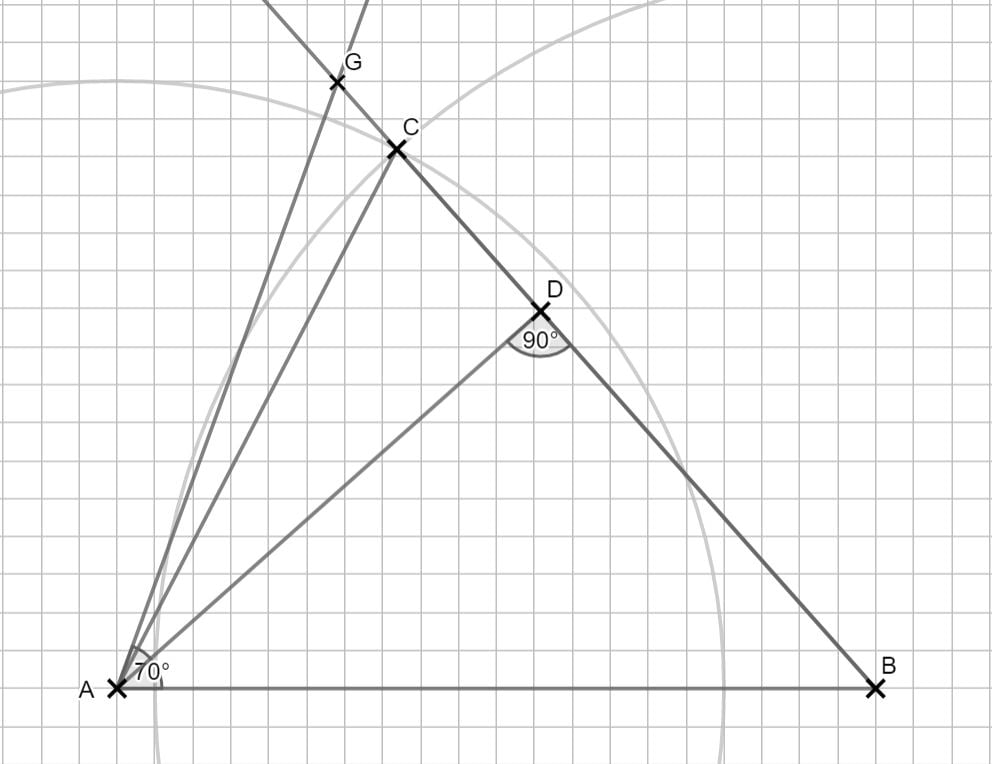
Um die Länge der Strecke [CG] berechnen zu können, benötigst du zuerst die Länge der Stecke [BG]:
\begin{align} &\overline{BG} \, mit \, dem \, Sinussatz: \\ \frac{\overline{BG}}{sin(\angle BAG)} &= \frac{\overline{AB}}{sin(\angle AGB)} \,\,\, |\cdot (\angle BAG) \\ \overline{BG} &= \frac{\overline{AB}}{sin(\angle AGB)} \cdot sin(\angle BAG) \\ \\ mit \angle AGB &= 180° – 70° – 48,36° \\ &= 61,64° \\ \\ \overline{BG} &= \frac{10}{sin(61,64°)} \cdot sin(70°) \\ \Rightarrow &\overline{BG} = 10,68 cm \\ \\ &\overline{CG} \, durch \, Subtraktion: \\ \overline{CG} &= \overline{BG} – \overline{BC} \\ &= 10,68 – 9,5 \\ \Rightarrow &\overline{CG} = 1,18 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu B2.4

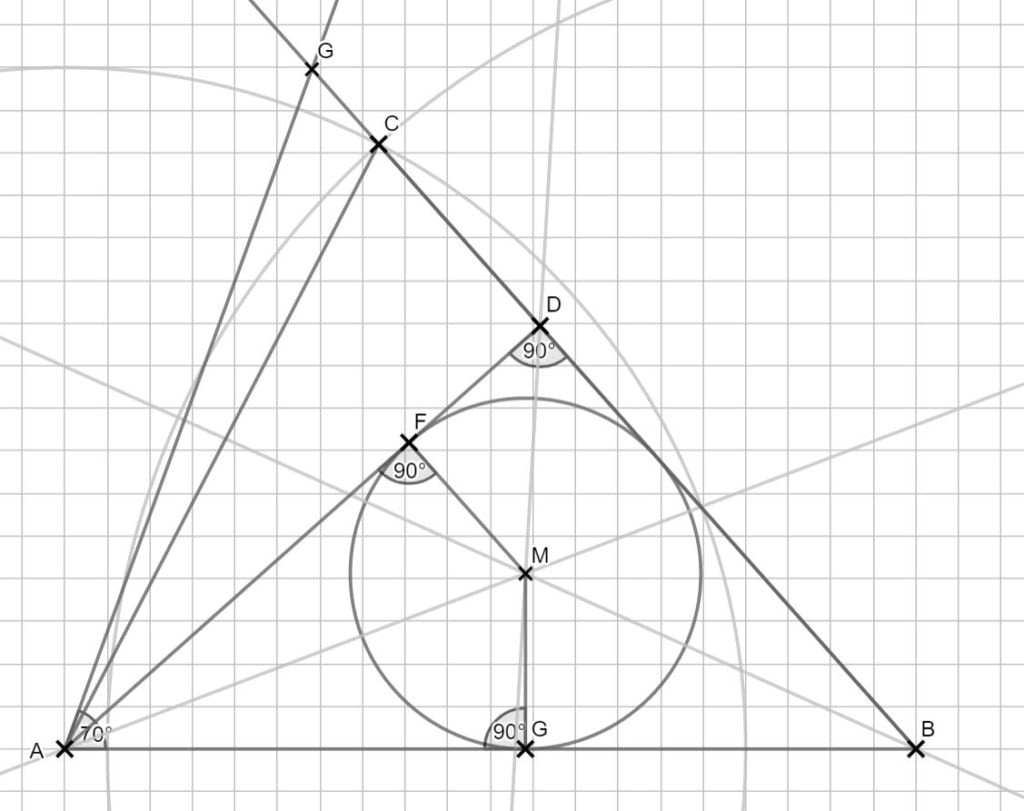
Zurück zum MAP-Hack:
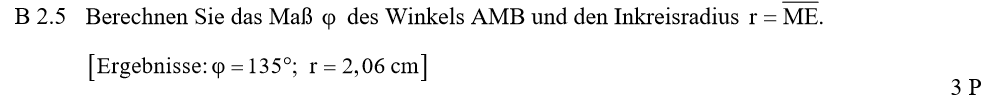
Lösung zu B2.5
\begin{align} &\varphi \, mit \, der \, Innenwinkelsumme: \\ \varphi &= 180° – 0,5 \cdot \beta – 0,5 \cdot \varepsilon \\ &= 180° – 0,5 \cdot 48,36° – 0,5 \cdot 41,64° \\ \Rightarrow & \varphi = 135° \end{align}
Für den Radius r benötigst du die Länge der Strecke [BM], welche du mit dem Sinussatz berechnen kannst.
\begin{align} & \overline{BM} \, mit \, dem \, Sinussatz: \\ \frac{\overline{BM}}{sin(0,5 \cdot \varepsilon)} &= \frac{\overline{AB}}{sin(\varphi)} \,\,\, | \cdot sin(0,5 \cdot \varepsilon) \\ \overline{BM} &= \frac{\overline{AB}}{sin(\varphi)} \cdot sin(0,5 \cdot \varepsilon) \\ &= \frac{10}{sin(135°)} \cdot sin(0,5 \cdot 41,64°) \\ \Rightarrow & \overline{BM} = 5,03 cm \\ \\ &r = \overline{ME} \, mit \, dem \, Sinus: \\ sin(0,5 \cdot \beta) &= \frac{\overline{ME}}{\overline{BM}} \,\,\, |\cdot \overline{BM} \\ \overline{ME} &= \overline{BM} \cdot sin(0,5 \cdot \beta) \\ &= 5,03 \cdot sin(0,5 \cdot 48,36°) \\ \Rightarrow &r = \overline{BM} = 2,06 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu 2.6
Um den gesuchten Flächeninhalt zu erhalten, benötigst du den Flächeninhalt des Drachen und ziehst davon den Flächeninhalt des Sektors ab. Um diese jeweils berechnen zu können, benötigst du die Länge der Strecke [AE] und den eingeschlossenen Winkel FME des Kreissektors:
\begin{align} & \overline{AE} \, mit \, dem \, Tangens: \\ tan(0,5 \cdot \varepsilon) &= \frac{\overline{BM}}{\overline{AE}} \,\,\, |\cdot \overline{AE} : tan(0,5 \cdot \varepsilon) \\ \overline{AE} &= \frac{\overline{BM}}{tan(0,5 \cdot \varepsilon)} \\ &= \frac{2,06}{tan(0,5 \cdot 41,64°)}\ \\ \Rightarrow &\overline{AE} = 5,42 cm \\ \\ &\angle FME \, mit \, der \, Innenwinkelsumme: \\ \angle FME &= 360° – 2 \cdot 90° – \varepsilon \\ &= 360° – 2 \cdot 90° – 41,64° \\ \Rightarrow &\angle FME = 138,36° \\ \\ &A \, durch \, Subktration: \\ A &= A_{Drache} – A_{Sektor}\\ &= 2 \cdot A_{Dreieck} – A_{Sektor} \\ &= 2 \cdot 0,5 \cdot 5,42 \cdot 2,06 – 2,06^2 \cdot \pi \cdot \frac{138,36°}{360°} \\ \Rightarrow &A = 6,04 cm^2 \end{align}
