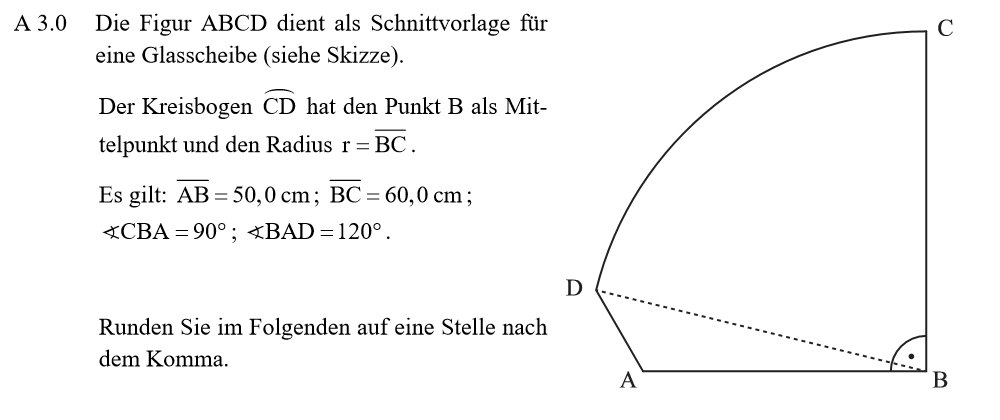
Lösung zu A3.1
\begin{align} &\angle ADB \, mit \, dem \, Sinussatz: \\ \frac{sin(\angle ADB)}{\overline{AB}} &= \frac{sin(\angle BAD)}{\overline{BD}} \,\,\, |\cdot \overline{AB} \\ sin(\angle ADB) &= \frac{sin(\angle BAD)}{\overline{BD}} \cdot \overline{AB} \\ &= \frac{sin(120°)}{60} \cdot 50 \\ \Rightarrow &\angle ADB = 46,2° \\ \\ &\angle DBA \, mit \, der \, Innenwinkelsumme: \\ \angle DBA &= 180° – 120° – 46,2° \\ \Rightarrow &\angle DBA = 13,8° \\ \\ &\overline{DA} \, mit \, dem \, Cosinussatz: \\ \overline{DA}^2 &= \overline{AB}^2 + \overline{BD}^2 – 2 \cdot \overline{AB} \cdot \overline{BD} \cdot cos( \angle DBA) \\ &= 50^2 + 60^2 – 2 \cdot 50 \cdot 60 \cdot cos(13,8°) \\ \Rightarrow &\overline{DA} = 16,5 cm \end{align}
Zurück zum MAP-Hack:

Lösung zu A3.2
\begin{align} &Bogenlänge \, b \, mit \, der \, Formel: \\ b &= 2 \cdot \overline{BC} \cdot \pi \cdot \frac{\angle CBD}{360°} \\ \\ mit &\angle CBD = \angle CBA – \angle DBA \\ &= \angle CBD = 90° – 13,8° = 76,2° \\ \\ b &= 2 \cdot 60 \cdot \pi \cdot \frac{76,2°}{360°} \\ \Rightarrow &b = 79,8 cm \\ \\ &Berechnung \, von \, t: \\ t &= \frac{b + \overline{DA}}{30} \\ &= \frac{79,8 + 16,5}{30} \\ \Rightarrow &t = 3,2 s \end{align}

Hallo, in der formelsammlung steht bei mir für die Bogenlänge: b= r*pi*my/360grad
Also ohne die 2* vor dem Radius..
Ja, es gibt die Formel mit 2 und 360° oder ohne und 180°. Da kann man ja Kürzen. Formel genau anschauen!
Hallo, in der formelsammlung steht bei mir für die Bogenlänge: b= r*pi*my/360grad
Also ohne die 2* vor dem Radius..
Ja, es gibt die Formel mit 2 und 360° oder ohne und 180°. Da kann man ja Kürzen. Formel genau anschauen!