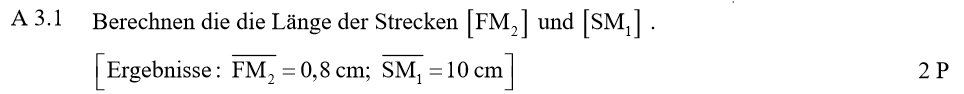
Lösung zu A3.1
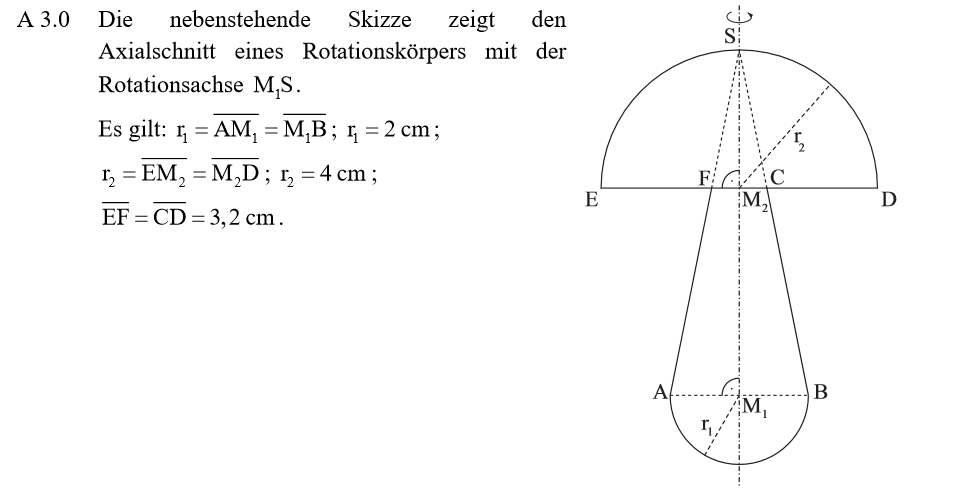
Die Strecke \(\overline{FM_2}\) lässt sich per Subtraktion aus den gegebenen Größen berechnen:
\begin{align} \overline{FM_2} &= \; \overline{EM_2} – \overline{EF}\\ &= \; 4 \text{ cm} – 3,2 \text{ cm}\\ &= \; 0,8 \text{ cm}. \end{align}
Die Strecke \(\overline{SM_1}\) lässt sich unter Ausnutzung des Vierstreckensatzes über die Dreiecke \(SAM_1 \) und \(SFM_2\) berechnen, da \(\overline{AM_1}\) und \(\overline{FM_2}\) parallel sind:
\begin{align} \frac{\; \overline{SM_1}\;}{ \overline{AM_1}} &= \; \frac{\; \overline{SM_2}\;}{ \overline{FM_2}}\\ \Rightarrow \qquad \qquad \overline{SM_1} &= \; \frac{ \;\overline{SM_2}\; }{ \overline{FM_2}} \cdot \overline{AM_1}\\ &= \; \frac{ 4 \text{ cm}}{ 0,8 \text{ cm}} \cdot 2 \text{ cm}\\ &= \; 10 \text{ cm} \end{align}
Zurück zum MAP-Hack:
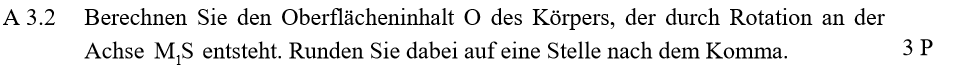
Lösung zu A3.2
Der Oberflächeninhalt setzt sich zusammen aus vier Flächen zusammen:
\begin{align} O = O_{\text{HKUGEL}} + O_{\text{hkugel}} + O_{\text{Ring}} + O_{\text{Mantel}} \end{align}
Diese sind:
\(1. \, O_{\text{HKUGEL}}\): Oberflächeninhalt der großen Halbkugel mit
Mittelpunkt \(M_2\) und Radius \(r_2\) ohne Schnittfläche
\(2. \, O_{\text{hkugel}}\): Oberflächeninhalt der kleinen Halbkugel mit
Mittelpunkt \(M_1\) und Radius \(r_1\) ohne Schnittfläche
\(3. \, O_{\text{Ring}}\): Kreisring an der Schnittfläche der großen
Kugel. Der Kreisring hat den Mittelpunkt \(M_2\), äußerem Radius \(r_2\) und innerem Radius \(\overline{FM_2}\). \( 4. \, O_{\text{Mantel}} \) Mantel des Kegelstumpfes: Dieser ergibt sich
aus der Subtraktion der Mäntel des großen Kegels \(O_{\text{KEGEL}}\)
und des kleinen Kegels \(O_{\text{kegel}}\) um die Rotationsachse
\(\overline{SM_1}\). Der große Kegel hat die Spitze in \(S\) und seine
Kreisgrundfläche den Mittelpunkt \(M_1\) und Radius \(r_1\). Der kleine Kegel hat ebenfalls die Spitze in \(S\) und dessen Kreisgrundfläche den Mittelpunkt \(M_2\) und Radius \(\overline {FM_2}\).
Für die Berechnung der Mäntel werden die Kanten \(\overline{AS}\) und \(\overline{SF}\) benötigt. Diese können über die Dreiecke \(SAM_1\) und \(SFM_2\) ermittelt werden, da die jeweils beiden anderen Seiten bekannt sind. Somit ergibt sich aus dem Satz des Pythagoras:
\begin{align} \overline{AS}^2 &= \;\overline{SM_1}^2 + \overline{AM_1}^2 \\ &= \;\sqrt{(10 \text{ cm})^2 + (2 \text{ cm})^2}\\ &\approx \; 10,2 \text{ cm}^2\ \\ \overline{SF}^2 &= \;\overline{FM_2}^2 + \overline{SM_2}^2\\ &= \;\sqrt{(4 \text{ cm})^2 + (0,8 \text{ cm})^2}\\ &\approx \; 4,1 \text{ cm}^2 \end{align}
So werden die Oberflächen berechnet:
\begin{align} O_{\text{HKUGEL}} &= \; \tfrac 12 \cdot \left( 4 \cdot \pi \cdot r_2^2 \right)\\ &= \; \tfrac 12 \cdot 4 \cdot \pi \cdot (4 \text{ cm})^2 \\ &\approx \; 100,5 \text{ cm}^2 \\ O_{\text{hkugel}} &= \; \tfrac 12 \cdot \left( 4 \cdot \pi \cdot r_2^2 \right) \\ &= \; \tfrac 12 \cdot 4 \cdot \pi \cdot (2 \text{ cm})^2 \\ &\approx \; 25,1 \text{ cm}^2 \\ O_{\text{Ring}} &= \; r_2^2\cdot \pi – \overline{M_2C}^2 \cdot \pi \\ &= \; (4 \text{ cm})^2\cdot \pi – (0,8 \text{ cm})^2 \cdot \pi \\ &\approx \; 48,3 \text{ cm}^2 \\ O_{\text{Mantel}} &= \; O_{\text{KEGEL}} – O_{\text{kegel}}\\ &= \; \left( r_1 \cdot \pi \cdot \overline{AS} \right) – \left( \overline{M_2C} \cdot \pi \cdot\overline {SF}\right) \\ &= \; \left( 2 \text{ cm} \cdot \pi \cdot 10,2 \text{ cm} \right) – \left( 0,8 \text{ cm} \cdot \pi \cdot 4,1 \text{ cm}\right) \\ &\approx \; 53,9 \text{ cm}^2 \end{align}
Somit erhalten wir als Endergebnis
\begin{align} O &= \; 100,5 \text{ cm}^2 + 25,1 \text{ cm}^2 + 48,3 \text{ cm}^ 2 + 53,9 \text{ cm}^2 \\ &= 227,8 \text{ cm}^2. \end{align}
Das Ergebnis in der offiziellen Lösungen ist \( O = 227,7 \text{cm}^2 \), nicht wie hier \( O = 227,8 \text{cm}^2 \). Der Unterschied in der Nachkommastelle ergibt sich aus Rundungen in den Zwischenschritten. Wie immer gilt in solchen Fällen: Beide Ergebnisse sind richtig und geben volle Punktzahl.
