

Lösung zu B1.1
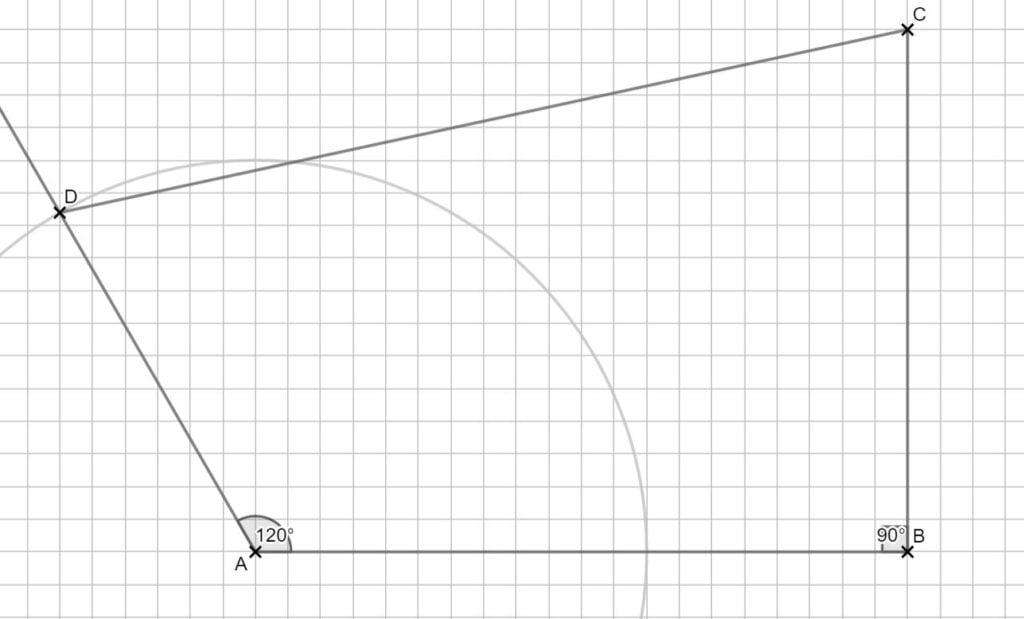
\begin{align} &\overline{BD} \text{ mit dem Cosinussatz:}\\
\overline{BD}^2 &= \overline{AB}^2 + \overline{AD}^2 – 2 \cdot \overline{AB} \cdot \overline{AD} \cdot cos(\angle BAD) \\
&= 10^2 + 6^2 – 2 \cdot 10 \cdot 6 cos(120°) \\
\Rightarrow \overline{BD} = 14 \text{ cm}\\
\\
&\angle DBA \text{ mit dem Sinussatz:}\\
\frac{sin(\angle DBA)}{\overline{AD}} &= \frac{sin(\angle BAD)}{\overline{BD}} \\
\frac{sin(\angle DBA)}{6} &= \frac{sin(120°)}{14} \,\,\, |\cdot 6\\
sin(\angle DBA) &= \frac{sin(120°)}{14} \cdot 6 \\
\Rightarrow &\angle DBA = 21,79° \end{align}
Zurück zum MAP-Hack:
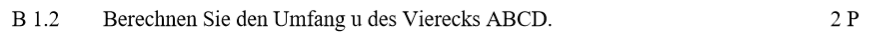
Lösung zu B1.2
Der Umfang setzt sich aus den vier Seitenlängen zusammen, wobei du nur \( \overline{CD} \) berechnen.
\begin{align} &\overline{CD} \text{ mit dem Cosinussatz:}\\
\overline{CD}^2 &= \overline{BD}^2 + \overline{BC}^2 – 2 \cdot \overline{BD}\cdot \overline{BC}\cdot cos(\angle CBD) \\
&= 14^2 + 8^2 – 2 \cdot 14 \cdot 8 \cdot cos(90° -21,79°) \\
\Rightarrow &\overline{CD} = 13,30 \text{ cm} \\
\\
&\text{Berechnung des Umfangs u:}\\
u &= \overline{AB} + \overline{BC} + \overline{CD} + \overline{AD}\\
&= 10 + 8 + 13,30 + 6 \\
\Rightarrow &u = 37,30 \text{ cm}\end{align}

Lösung zu B1.3
Zeichne zuerst den Kreisbogen und die Strecke [AF] ein.
Der Kreis berührt die Strecke [BD], im Berührpunkt ist also ein 90°-Winkel. Mit diesem kannst du die Länge der Strecke [AF] ausrechnen. Warum [AF]? Es ist ein Teilergebnis und du wirst es brauchen:
\begin{align} &\overline{AF} \text{ mit dem Sinus:}\\
sin(\angle DBA) &= \frac{\, \overline{AF} \,}{\overline{AB}} \\
sin(21,79°) &= \frac{\, \overline{AF} \,}{10} \,\,\, |\cdot 10\\
\overline{AF} &= sin(21,79°) \cdot 10 \\
\Rightarrow &\overline{AF} = 3,17 \text{ cm} \end{align}
Der Flächeninhalt ergibt sich, indem man vom Dreieck ABF den Kreissektor abzieht.
\begin{align} A_{\triangle} &= \frac{1}{2} \cdot \overline{AF} \cdot \overline{AB} \cdot sin(\angle BAF)\\
&= \frac{1}{2} \cdot 3,71 \cdot 10 \cdot sin(180° – 90° – 21,79°) \\
\Rightarrow &A_{\triangle} = 17,22
\\
A_{Sektor} &= \overline{AF}^2 \cdot \pi \cdot \frac{\angle BAF}{360°}\\
&= 3,71^2 \cdot \pi \cdot \frac{180° – 90° -21,79°}{360°} \\
\Rightarrow &A_{Sektor} = 8,19\\
\\
A &= A_{\triangle} – A_{Sektor} \\
&= 17,22 – 8,19 \\
\Rightarrow &A = 9,03 \text{ cm}^2 \end{align}
Zurück zum MAP-Hack:

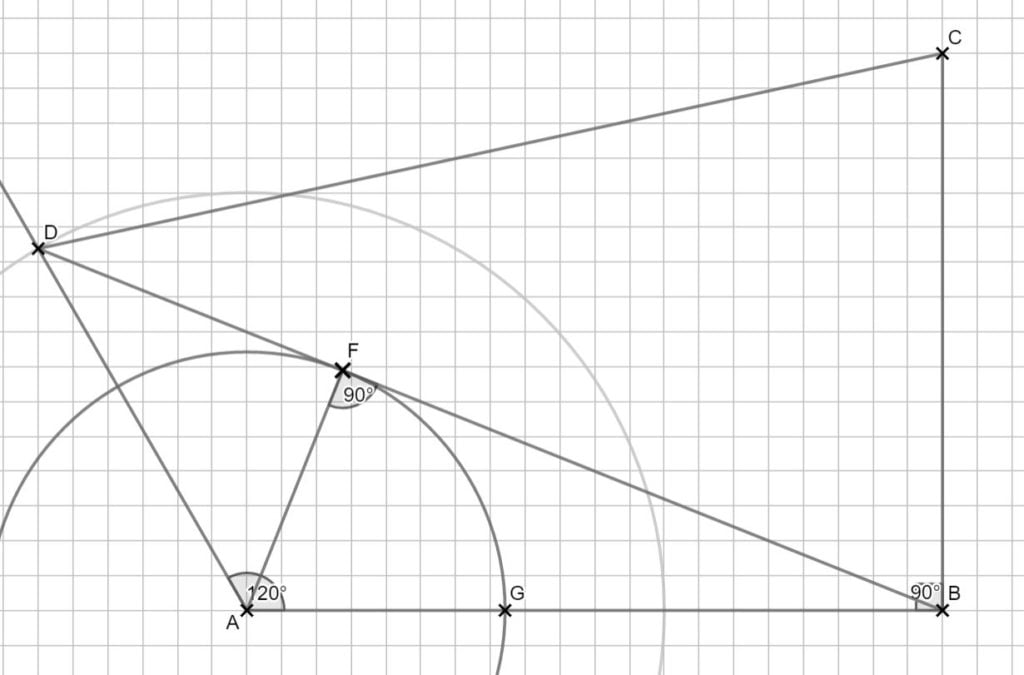
Lösung zu B1.4
Zeichne zerst die Strecke \( [H_1 C] \) ein.
\begin{align} &\overline{H_n C} \text{ mit dem Cosinussatz:}\\
\overline{H_n C}^2 &= \overline{H_n B}^2 + \overline{BC}^2 – 2 \cdot \overline{H_n B} \cdot \overline{BC} \cdot cos(\angle CBD) \\
&= x^2 + 8^2 – 2 \cdot x \cdot 8 \cdot cos(90° – 21,79°) \,\,\, |\sqrt{} \\
\Rightarrow &\overline{H_n C}(x) = \sqrt{x^2 – 5,94x + 64} \text{cm}\end{align}

Lösung zu B1.5
Weil im Punkt \( H_0 \) die minimale Länge gilt, ist dort ein rechter Winkel und du kannst mit Sinus, Cosinus und Tangens rechnen.
\begin{align} &x \text{ mit dem Cosinus:}\\
cos(\angle CBD) &= \frac{\, \overline{B H_0} \,}{\overline{BC}}\,\,\, \text{ mit } \overline{B H_0} = x \\
cos(90° – 21,79°) &= \frac{\, x\,}{8} \,\,\, |\cdot 8\\
x &= cos(90°-21,79°) \cdot 8 \\
\Rightarrow &x = 2,97 \\
\\
&\text{Einsetzen in die Formel für die Streckenlänge:}\\
\overline{H_n C}(x) &= \sqrt{x^2 – 5,95 \cdot x + 64}\\
\overline{H_0 C}(2,97) &= \sqrt{2,97^2 – 5,95 \cdot 2,97 + 64} \\
\Rightarrow &\overline{H_0 C} = 7,43 \text{cm} \end{align}

Lösung zu B1.6

Zuerst berechnest du die Länge der Strecke [BF] im Dreieck ABF um damit weiterzurechnen:
\begin{align} &\overline{BF} \text{ mit dem Cosinus in ABF:}\\
cos(\angle DBA) &= \frac{\, \overline{BF} \,}{\overline{AB}} \,\,\, |\cdot \overline{AB} \\
\overline{BF} &= cos(\angle DBA) \cdot \overline{AB} \\
&= cos(21,79°) \cdot 10 \\
\Rightarrow &\overline{BF} = 9,29 \end{align}
Von hieraus kannst du z.b. die Länge der Strecke [FC] mit dem Cosinussatz berechnen:
\begin{align} &\overline{FC} \text{ mit dem Cosinussatz:} \\
\overline{FC}^2 &= \overline{BC}^2 + \overline{FB}^2 – 2 \cdot \overline{BC} \cdot \overline{FB} \cdot cos(CBF) \\
&= 8^2 + 9,29^2 – 2 \cdot 8 \cdot 9,29 \cdot cos(90° – 21,79°) \,\,\, |\sqrt{}\\
\Rightarrow &\overline{FC} = 9,75 \text {cm} \end{align}
Alle drei Seiten haben unterschiedliche Längen, das Dreieck ist nicht gleichschenklig.
