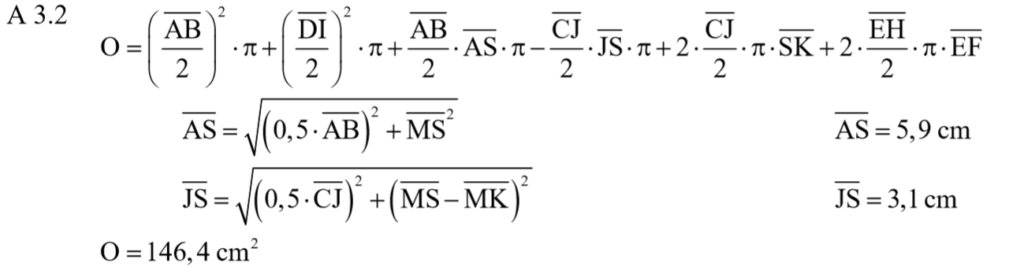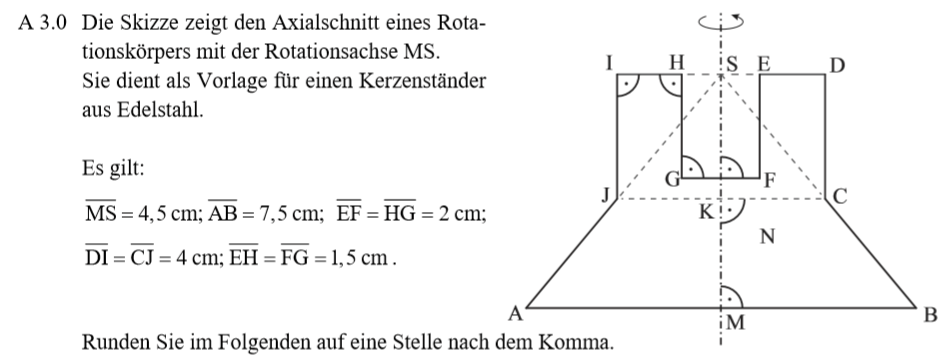
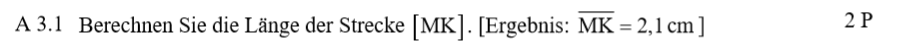
Lösung zu A3.1
\begin{align} \overline{MK} \text{ mit dem Vierstreckensatz:}\\
\frac{\, \overline{SK} \,}{\overline{MS}} &= \frac{\, \overline{CJ} \,}{\overline{AB}} \\
\frac{\, \overline{MS} – \overline{MK} \,}{\overline{MS}} &= \frac{\, \overline{CJ} \,}{\overline{AB}}\\
\frac{\, 4,5 – \overline{MK}}{4,5} &= \frac{4}{7,5} \,\,\, |\cdot 4,5\\
4,5 – \overline{MK} &= \frac{4}{7,5} \cdot 4,5 \,\,\, |- 4,5 \,\,\, |\cdot (-1)\\
\overline{MK} &= 2,1 \text{cm}\end{align}
Zurück zum MAP-Hack:
Lösung zu A3.2
Dem Ersteller dieser Aufgabe möchte ich gerne die Hand schütteln. Wer meint, dass ewiges Einsetzen in Formeln mathematisches Können beweist, der … lassen wir das. Hier ist der Überblick über die Aufgabe. Ich würde die Teiloberflächen berechnen und anschließend addieren, weil die Rechnung zu lang für den Taschenrechner wird. Wenn so eine Aufgabe in deiner Prüfung vorkommt, mache sie ganz am Ende. Die Chance, dass du dich vertippst ist hoch und es dauert relativ lange. Mein Tipp ist hier also nicht die richtige Lösung, sondern das strategische Auslassen von Aufgaben bzw die Bearbeitung am Ende.