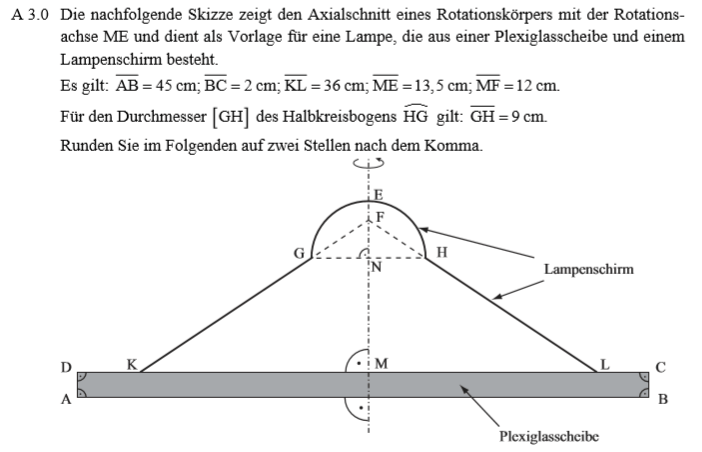
Lösung zu A3.1
\begin{align} V &= (0,5 \cdot \overline{AB})^2 \cdot \pi \cdot \overline{BC} \\
&= (0,5 \cdot 45)^2 \cdot \pi \cdot 2\\
\Rightarrow &V = 3180,86 \text{cm}^3 \end{align}
Zurück zum MAP-Hack:
Lösung zu A3.2
Die Fläche setzt sich aus der Oberfläche der Halbkugel und der Mantelfläche des Kegelstumpfs zusammen.
\begin{align} &\text{Ziel: } A = M_{Kegel groß} – M_{Kegel klein} + 0,5 \cdot O_{Kugel}\\
\\
\overline{ML} &= 0,5 \cdot \overline{KL} = 0,5 \cdot 36 = 18 \text{cm} \\
\overline{NH} &= 0,5 \cdot \overline{NH} = 0,5 \cdot 9 = 4,5 \text{cm}\\
\\
&\overline{FL} \, \text{mit dem Satz des Pythagoras:}\\
\overline{FL}^2 &= \overline{MF}^2 + \overline{ML} \\
&= 12^2 + 18^2 \\
\Rightarrow &\overline{FL} = 21,63 \text{cm}\\
\\
&\overline{FH} \, \text{mit dem Vierstreckensatz:}\\
\frac{\overline{FH}}{\overline{FL}} &= \frac{\overline{NH}}{\overline{ML}} \\
\frac{\overline{FH}}{21,63} &= \frac{4,5}{18} \,\,\, |\cdot 21,63\\
\overline{FH} &= \frac{4,5}{18} \cdot 21,63 \\
\Rightarrow &\overline{FH} = 5,41 \text{cm}\\
\\
&\text{Berechnung der Oberfläche:}\\
A &= M_{Kegel groß} – M_{Kegel klein} + 0,5 \cdot O_{Kugel}\\
&= \overline{ML} \cdot \pi \cdot \overline{FL} – \overline{NH} \cdot \pi \cdot \overline{FH} + 0,5 \cdot 4 \cdot \overline{NH}^2 \cdot \pi \\
&= 18 \cdot \pi \cdot 21,63 – 4,5 \cdot \pi \cdot 5,41 + 0,5 \cdot 4 \cdot 4,5^2 \cdot \pi \\
\Rightarrow &A = 1273,90 \text{cm}^2 \end{align}
