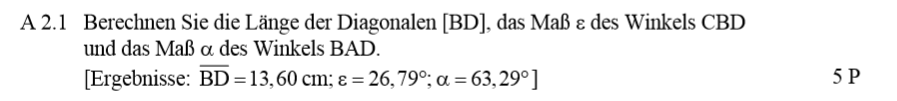
Lösung zu A2.1
\begin{align} &\overline{BD} \, \text{mit dem Cosinussatz:}\\
\overline{BD}^2 &= \overline{CD}^2 + \overline{BC}^2 – 2 \cdot \overline{CD} \cdot \overline{BC} \cdot cos(\angle DCB) \\
&= 8^2 + 7^2 – 2 \cdot 8 \cdot 7 \cdot cos(130°)\\
\Rightarrow &\overline{BD} = 13,60 \text{cm} \\
\\
&\varepsilon \text{ mit dem umgeformten Cosinussatz:}\\
cos(\varepsilon) &= \frac{\overline{BC}^2 + \overline{BD}^2 – \overline{CD}^2}{2 \cdot \overline{BC} \cdot \overline{BD}}\\
&= \frac{7^2 + 13,60^2 – 8^2}{2 \cdot 7 \cdot 13,60}\\
\Rightarrow &\varepsilon = 26,79° \end{align}
Um \( \alpha \) mit dem Sinussatz berechnen zu können, benötigst du das Maß des Winkel DBA. Du kannst ihn mit aus der Innenwinkelsumme bestimmen.
\begin{align} &\angle DBA \text{ mit der Innenwinkelsumme:}\\
\angle BDC &= 180° – \angle DCB – \varepsilon \\
&= 180° – 130° – 26,79° \\
\Rightarrow &\angle DBA = 23,21° \\
& \text{außerdem gilt:}\, \angle DBA = \angle BDC \text{ (Wechselwinkel)}\\
\\
&\alpha \text{ mit dem Sinussatz:} \\
\frac{sin(\alpha)}{\overline{BD}} &= \frac{sin(\angle DBA)}{\overline{AD}}\\
\frac{sin(\alpha)}{13,60} &= \frac{sin(23,21°)}{6}\,\,\, |\cdot 13,60 \\
sin(\alpha) &= \frac{sin(23,21°)}{6} \cdot 13,60 \\
\Rightarrow &\alpha = 63,29° \end{align}
Zurück zum MAP-Hack:

Lösung zu A2.2
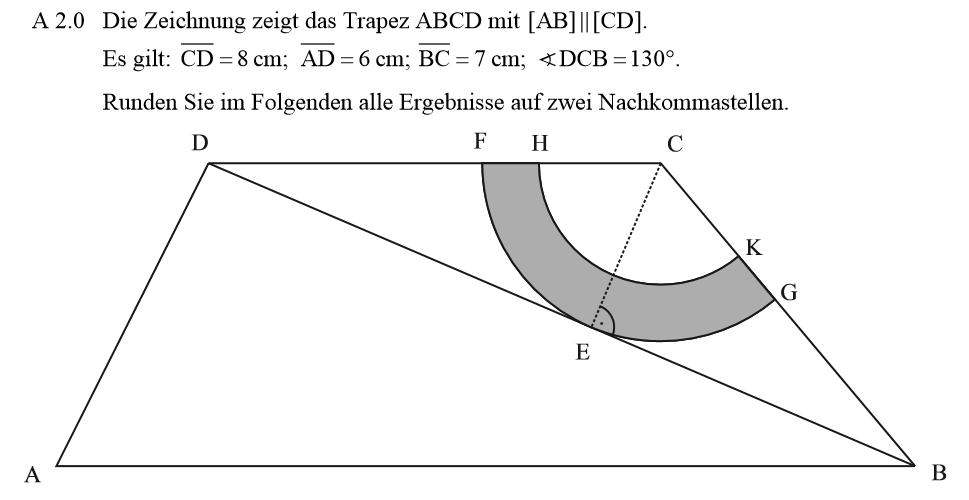
Weil der Kreisbogen die Diagonale [BD] in E berührt, ist der Winkel bei E 90°. Du darfst also mit Sinus, Cosinus und Tangens arbeiten.
\begin{align} &\overline{CE} \text{ mit dem Sinus:}\\
sin(\varepsilon) &= \frac{\, \overline{CE}\,}{\overline{BC}} \\
sin(26,79°) &= \frac{\overline{CE}}{7} \,\,\, |\cdot 7 \\
\overline{CE} &= sin(26,79°) \cdot 7 \\
\Rightarrow &\overline{CE} = 3,16 \text{cm}\end{align}
Zurück zum MAP-Hack:

Lösung zu A2.3
Der Flächeninhalte entsteht, indem du vom Flächeninhalt des großen Kreissektors mit Radius [CE] den Flächeninhalt des Kreissektors mit dem kleinen Radius abziehst. Im Zwischenteil klammere ich den Winkel und das Pi aus, das musst du aber nicht machen.
\begin{align} A &= A_{groß} – A_{klein} \\
&= \frac{\angle DCB}{360°} \cdot \overline{CE}^2 \cdot \pi- \frac{\angle DCB}{360°} \cdot (\overline{CE} – \overline{FH})^2 \cdot pi \\
&= \frac{\angle DCB}{360°} \cdot pi \cdot (\overline{CE}^2 – (\overline{CE} – \overline{FH})^2) \\
&= \frac{130°}{360°} \cdot \pi \cdot (3,16^2 – (3,16 – 1)^2 )\\
\Rightarrow &A = 6,04 \text{cm}^2 \end{align}
Jetzt brauchst du noch den Flächeninhalt des Trapezes, das sich aus zwei Dreiecken zusammensetzt. Hierfür brauchst du das Winkelmaß von ADB.}
\begin{align} &\angle ABD \text{ mit der Innenwinkelsumme:}\\
\angle ADB &= 180° – \alpha – \angle DBA \\
&= 180° – 63,29° – 23,21° \\
\Rightarrow &\angle ADB = 93,50° \\
\\
&A_{Trapez} \, \text{aus zwei Dreiecken:}\\
A_{Trapez} &= A_{\triangle ABD} + A_{\triangle DBC}\\
&= 0,5 \cdot \overline{AD} \cdot \overline{BD} \cdot sin(\angle ADB) + 0,5 \cdot \overline{CD} \cdot \overline{BC} \cdot sin(\angle DCB)\\
&= 0,5 \cdot 6 \cdot 13,60 \cdot sin(93,50°) + 0,5 \cdot 8 \cdot 7 \cdot sin(130°)\\
\Rightarrow &A_{Trapez} = 62,17 \text{cm}^2 \\
\\
&p \text{ über die Prozentformel:}\\
p &= \frac{\text{Anteil}}{\text{Ganze}} \cdot 100 \% \\
&= \frac{\, A\, }{A_{Trapez}} \cdot 100 \% \\
&= \frac{6,04}{62,17} \cdot 100 \% \\
\Rightarrow &p = 9,72 \% \end{align}
